摘要：.所以是直线与曲线的一个切点, ----10分所以直线l与曲线S相切且至少有两个切点,
网址：http://m.1010jiajiao.com/timu_id_192299[举报]
以下是关于圆锥曲线的四个命题：
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
-
=1与椭圆
+y2=1有相同的焦点；
④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为
查看习题详情和答案>>
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为
②③④
②③④
（写出所以真命题的序号）．以下是关于圆锥曲线的四个命题：
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
-
=1与椭圆
+y2=1有相同的焦点；
④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为______（写出所以真命题的序号）．
查看习题详情和答案>>
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为______（写出所以真命题的序号）．
以下是关于圆锥曲线的四个命题：
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
与椭圆
有相同的焦点；
④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为 （写出所以真命题的序号）． 查看习题详情和答案>>
①设A、B为两个定点，k为非零常数，若PA-PB=k，则动点P的轨迹是双曲线；
②方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
③双曲线
与椭圆有相同的焦点；④以过抛物线的焦点的一条弦AB为直径作圆，则该圆与抛物线的准线相切．
其中真命题为 （写出所以真命题的序号）． 查看习题详情和答案>>
以下五个命题中：
①若两直线平行，则两直线斜率相等；
②设F1、F2为两个定点，a为正常数，且||PF1|-|PF2||=2a，则动点P的轨迹为双曲线；
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
④对任意实数k，直线l：kx-y+1-k=0与圆x2+y2-2y-4=0的位置关系是相交；
⑤P为椭圆
+
=1（a＞b＞0）上一点，F为它的一个焦点，则以PF为直径的圆与以长轴为直径的圆相切．
其中真命题的序号为
查看习题详情和答案>>
①若两直线平行，则两直线斜率相等；
②设F1、F2为两个定点，a为正常数，且||PF1|-|PF2||=2a，则动点P的轨迹为双曲线；
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
④对任意实数k，直线l：kx-y+1-k=0与圆x2+y2-2y-4=0的位置关系是相交；
⑤P为椭圆
| x2 |
| a2 |
| y2 |
| b2 |
其中真命题的序号为
③④⑤
③④⑤
．（写出所有真命题的序号）
，
，
为常数，离心率为
的双曲线
：
上的动点
到两焦点的距离之和的最小值为
，抛物线
：
的焦点与双曲线的一顶点重合。(Ⅰ)求抛物线的方程；（Ⅱ）过直线
：
（
为负常数）上任意一点
向抛物线引两条切线，切点分别为
、
，坐标原点
恒在以
为直径的圆内，求实数的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为，离心率为，则长轴长为2，故双曲线的上顶点为
，所以抛物线的方程
第二问中，为
，
，
，
故直线
的方程为
，即
，
所以
，同理可得：
借助于根与系数的关系得到即
，
是方程
的两个不同的根，所以
由已知易得
，即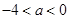
解：(Ⅰ)由已知易得双曲线焦距为，离心率为，则长轴长为2，故双曲线的上顶点为，所以抛物线的方程
（Ⅱ）设为，，，
故直线的方程为，即，
所以，同理可得：，
即，是方程的两个不同的根，所以
由已知易得
，即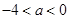
查看习题详情和答案>>