摘要:又.h(2)=ln2-1<0.∴h(x)与x轴有两个交点∴过点的切线.
网址:http://m.1010jiajiao.com/timu_id_192251[举报]
(2012•淄博一模)在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的
倍后得到点Q(x,
y),且满足
•
=1.
(I)求动点P所在曲线C的方程;
(II)过点B作斜率为-
的直线l交曲线C于M、N两点,且
+
+
=
,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
查看习题详情和答案>>
| 2 |
| 2 |
| AQ |
| BQ |
(I)求动点P所在曲线C的方程;
(II)过点B作斜率为-
| ||
| 2 |
| OM |
| ON |
| OH |
| 0 |
已知函数f(x)=alnx-x2.
(1)当a=2时,求函数y=f(x)在[
,2]上的最大值;
(2)令g(x)=f(x)+ax,若y=g(x)在区让(0,3)上不单调,求a的取值范围;
(3)当a=2时,函数h(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,又y=h′(x)是y=h(x)的导函数.若正常数α,β满足条件α+β=1,β≥α.证明h′(αx1+βx2)<0.
查看习题详情和答案>>
(1)当a=2时,求函数y=f(x)在[
| 1 | 2 |
(2)令g(x)=f(x)+ax,若y=g(x)在区让(0,3)上不单调,求a的取值范围;
(3)当a=2时,函数h(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,又y=h′(x)是y=h(x)的导函数.若正常数α,β满足条件α+β=1,β≥α.证明h′(αx1+βx2)<0.
(2012•黄浦区一模)已知两点A(-1,0)、B(1,0),点P(x,y)是直角坐标平面上的动点,若将点P的横坐标保持不变、纵坐标扩大到
倍后得到点Q(x,
y)满足
•
=1.
(1)求动点P所在曲线C的轨迹方程;
(2)过点B作斜率为-
的直线l交曲线C于M、N两点,且满足
+
+
=
,又点H关于原点O的对称点为点G,试问四点M、G、N、H是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
查看习题详情和答案>>
| 2 |
| 2 |
| AQ |
| BQ |
(1)求动点P所在曲线C的轨迹方程;
(2)过点B作斜率为-
| ||
| 2 |
| OM |
| ON |
| OH |
| 0 |
记定义在[-1,1]上的函数f(x)=x2+px+q(p,q∈R)的最大值与最小值分别为M,m.又记h(p)=M-m.
(Ⅰ)当0≤p≤2时,求M、m(用p,q表示),并证明h(p)≥1;
(Ⅱ)写出h(p)的解析式(不必写出求解过程);
(Ⅲ)在所有形如题设的函数f(x)中,求出这样的f(x),使得|f(x)|的最大值为最小. 查看习题详情和答案>>
(Ⅰ)当0≤p≤2时,求M、m(用p,q表示),并证明h(p)≥1;
(Ⅱ)写出h(p)的解析式(不必写出求解过程);
(Ⅲ)在所有形如题设的函数f(x)中,求出这样的f(x),使得|f(x)|的最大值为最小. 查看习题详情和答案>>
如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面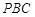 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

查看习题详情和答案>>