摘要:解(1)当------2分
网址:http://m.1010jiajiao.com/timu_id_192147[举报]
解答下列各题:
(1)请作出下列函数的大致图象
①y=
如图1;
②y=log3
如图2.

(2)如图

图甲中阴影部分表示的集合为
图乙表示的函数解析式可以为
查看习题详情和答案>>
(1)请作出下列函数的大致图象
①y=
|
②y=log3
| 1 |
| x+1 |

(2)如图

图甲中阴影部分表示的集合为
(CUB)∩A∪(B∩C)
(CUB)∩A∪(B∩C)
;图乙表示的函数解析式可以为
f(x)=
|
f(x)=
.
|
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半,现在从该盒中随机取出一球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数Y的分布列.
查看习题详情和答案>>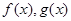 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当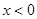 时,
时, 且
且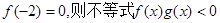 的解集为
的解集为
A.(-2,0)∪(2,+∞) B.(-2,0)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-∞,-2)∪(0,2)
查看习题详情和答案>>
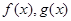 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当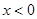 时,
时,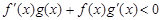
且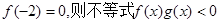 的解集为 ( )
的解集为 ( )
A.(-2,0)∪(2,+∞) B.(-2,0)∪(0,2)
C.(-∞,-2)∪(2,+∞)YCY D.(-∞,-2)∪(0,2)
查看习题详情和答案>>
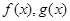 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当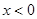 时
时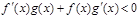 且
且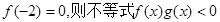 的解集为( )
的解集为( )
| A.(-2,0)∪(2,+∞) |
| B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) |
| D.(-∞,-2)∪(0,2) |