题目内容
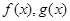 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当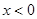 时
时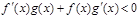 且
且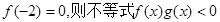 的解集为( )
的解集为( )
| A.(-2,0)∪(2,+∞) |
| B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) |
| D.(-∞,-2)∪(0,2) |
A
解析试题分析:设F(x)=f (x)g(x),当x<0时,?
∵F′(x)=f′(x)g(x)+f (x)g′(x)>0.
∴F(x)在当x<0时为增函数.?
∵F(-x)=f (-x)g (-x)=-f (x)•g (x).=-F(x).?
故F(x)为(-∞,0)∪(0,+∞)上的奇函数.?
∴F(x)在(0,+∞)上亦为增函数.?
已知g(-3)=0,必有F(-3)=F(3)=0.?
构造如图的F(x)的图象,可知
F(x)<0的解集为x∈(-∞,-3)∪(0,3).?
故选D.
考点:利用导数研究函数的单调性..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 的图象在点
的图象在点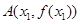 与点
与点 处的切线互相垂直,
处的切线互相垂直,
并交于点 ,则点
,则点 的坐标可能是( )
的坐标可能是( )
A. | B. | C. | D. |
设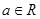 ,函数
,函数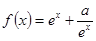 的导函数
的导函数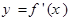 是奇函数,若曲线
是奇函数,若曲线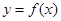 的一条切线的斜率为
的一条切线的斜率为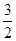 ,则切点的横坐标是( )
,则切点的横坐标是( )
A.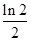 | B. | C.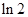 | D.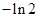 |
函数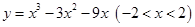 有( )
有( )
A.极大值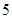 ,极小值 ,极小值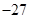 | B.极大值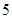 ,极小值 ,极小值 |
C.极大值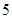 ,无极小值 ,无极小值 | D.极小值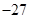 ,无极大值 ,无极大值 |
已知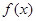 为
为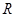 上的可导函数,且
上的可导函数,且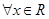 ,均有
,均有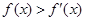 ,则以下判断正确的是
,则以下判断正确的是
A.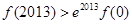 | B.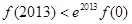 |
C.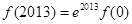 | D.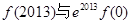 大小无法确定 大小无法确定 |
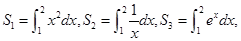 若 ,则s1,s2,s3的大小关系为( )
若 ,则s1,s2,s3的大小关系为( )
A.s1<s2<s3| B.s2<s1<s3 | C.s2<s3<s1 | D.s3<s2<s1 | |
函数y=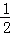 x2﹣lnx的单调递减区间为( )
x2﹣lnx的单调递减区间为( )
| A.(﹣1,1] | B.(0,1] |
| C.[1,+∞) | D.(0,+∞) |
已知二次函数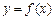 的图象如图所示,则它与
的图象如图所示,则它与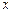 轴所围图形的面积为( )
轴所围图形的面积为( )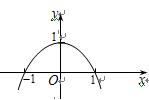
A.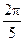 |
B.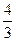 |
C.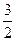 |
D.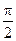 |
已知函数 在区间[-1,2]上是减函数,那么b+c( )
在区间[-1,2]上是减函数,那么b+c( )
A.有最大值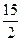 |
B.有最大值-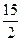 |
C.有最小值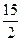 |
D.有最小值-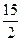 |