题目内容
解答下列各题:
(1)请作出下列函数的大致图象
①y=
如图1;
②y=log3
如图2.

(2)如图

图甲中阴影部分表示的集合为
图乙表示的函数解析式可以为
(1)请作出下列函数的大致图象
①y=
|
②y=log3
| 1 |
| x+1 |

(2)如图

图甲中阴影部分表示的集合为
(CUB)∩A∪(B∩C)
(CUB)∩A∪(B∩C)
;图乙表示的函数解析式可以为
f(x)=
|
f(x)=
.
|
分析:(1)①利用二次函数和幂函数的图象画法即可画出;
②先画出函数y=log3x的图象,再利用图象的变换即可画出.
(2)图甲利用集合的交、并、补即可表示出;
图乙根据图象的形状即可得出相应的函数的解析式.
②先画出函数y=log3x的图象,再利用图象的变换即可画出.
(2)图甲利用集合的交、并、补即可表示出;
图乙根据图象的形状即可得出相应的函数的解析式.
解答:解:(1)①作出图象如图所示: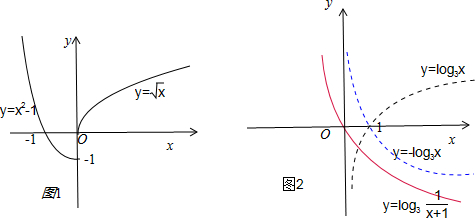
②先作出函数y=log3x的图象,再作出函数y=-log3x,将其向左平移一个单位即得到函数y=-log3(x+1)=log3
的图象:
(2)图甲中的阴影一部分是CUB∩A,另一部分是B∩C,
故图甲中阴影部分表示的集合为是(CUB∩A)∪B∩C;
图乙中的函数由三部分组成,
当x≤-1时,其图象与x轴平行且经过点(-1,-1),∴f(x)=-1;
当-1<x≤1时,其图象经过点(0,0)和(1,1),∴f(x)=x;
当x≥1时,其图象经过点(1,1),且单调递减与x轴无限接近,故f(x)=
.
综上可知:f(x)=
.
故答案(1)如图1、2;(2)图甲为(CUB∩A)∪B∩C;图乙为:f(x)=
.

②先作出函数y=log3x的图象,再作出函数y=-log3x,将其向左平移一个单位即得到函数y=-log3(x+1)=log3
| 1 |
| x+1 |
(2)图甲中的阴影一部分是CUB∩A,另一部分是B∩C,
故图甲中阴影部分表示的集合为是(CUB∩A)∪B∩C;
图乙中的函数由三部分组成,
当x≤-1时,其图象与x轴平行且经过点(-1,-1),∴f(x)=-1;
当-1<x≤1时,其图象经过点(0,0)和(1,1),∴f(x)=x;
当x≥1时,其图象经过点(1,1),且单调递减与x轴无限接近,故f(x)=
| 1 |
| x |
综上可知:f(x)=
|
故答案(1)如图1、2;(2)图甲为(CUB∩A)∪B∩C;图乙为:f(x)=
|
点评:熟练掌握函数的图象的画法与变换和性质是解题的关键.

练习册系列答案
相关题目
 一次函数f(x)=mx+n与指数型函数g(x)=ax+b(a>0,a≠1)的图象交于两点A(0,1),B(1,2),解答下列各题:
一次函数f(x)=mx+n与指数型函数g(x)=ax+b(a>0,a≠1)的图象交于两点A(0,1),B(1,2),解答下列各题: