摘要:(河南省许昌市上期末质量评估)设f(x)=.若f (x)存在.则常数a= .答案:-2
网址:http://m.1010jiajiao.com/timu_id_191684[举报]
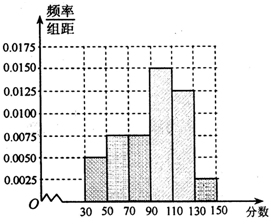 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:(I)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(II)若用分层抽样的方法从分数在[30,50)和[130,150]的学生中共抽取3人,该3人中成绩在[130,150]的有几人?
(III)在( II)中抽取的3人中,随机抽取2人,求分数在[30,50)和[130,150]各1人的概率.
(2013•鹰潭一模)某校在高三年级上学期期末考试数学成绩中抽取n个数学成绩进行分析,全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组[120,130],下表是按上述分组方法得到的频率分布表:
(1)求n及分布表中x,y,z的值;
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.
查看习题详情和答案>>
| 分 组 | 频 数 | 频 率 |
| [80,90) | x | 0.04 |
| [90,100) | 9 | y |
| [100,110) | z | 0.38 |
| [110,120) | 17 | 0.34 |
| [120,130] | 3 | 0.06 |
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.
(2013•唐山二模)某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年纪学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中语文、外语两科成绩至少有一科优秀的个数为X,求X的分布列和期望E(X).
附:K2=
.
查看习题详情和答案>>
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年纪学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中语文、外语两科成绩至少有一科优秀的个数为X,求X的分布列和期望E(X).
| p(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
 某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图:(Ⅰ)从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学,求成绩为90分的同学被抽中的概率;
(Ⅱ)学校规定:成绩不低于85分的为优秀,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(Ⅲ)从乙班高等数学成绩不低于85分的同学中抽取2人,成绩不低于90分的同学得奖金100元,否则得奖金50元,记ξ为这2人所得的总奖金,求ξ的分布列和数学期望.
 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分