摘要:(1)是否存在k.使对任意m>0.总有成立?若存在.求出所有k的值,
网址:http://m.1010jiajiao.com/timu_id_183096[举报]
我们规定:对于任意实数A,若存在数列{an}和实数x(x≠0),使得A=a1+a2x+a3x2+…+anxn-1,则称数A可以表示成x进制形式,简记为:A=
.如:A=
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
(1)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,ak+1=
,k∈N*,bn=
(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(3)若常数t满足t≠0且t>-1,dn=
,求
.
查看习题详情和答案>>
| . |
| x\~(a1)(a2)(a3)…(an-1)(an) |
| . |
| 2\~(-1)(3)(-2)(1) |
(1)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,ak+1=
| 1 |
| 1-ak |
| . |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
(3)若常数t满足t≠0且t>-1,dn=
| . | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
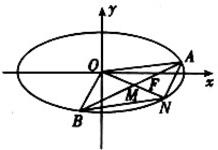
如图,已知椭圆C:
+
=
(m>0),经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
(1)是否存在k,使对任意m>0,总有
+
=
成立?若存在,求出所有k的值;
(2)若
•
=-
(m3+4m),求实数k的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
| x2 |
| 5 |
| y2 |
| 3 |
| m2 |
| 2 |
(1)是否存在k,使对任意m>0,总有
| OA |
| OB |
| ON |
(2)若
| OA |
| OB |
| 1 |
| 2 |
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,已知抛物线C:y2=2px(p>0)的准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点.
如图,已知抛物线C:y2=2px(p>0)的准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点.(Ⅰ)F为抛物线C的焦点,若
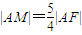 ,求k的值;
,求k的值;(Ⅱ)是否存在这样的k,使得对任意的p,抛物线上C总存在点Q,使得QA⊥QB,若存在,求出k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
(2008•奉贤区模拟)我们规定:对于任意实数A,若存在数列{an}和实数x(x≠0),使得A=a1+a2x+a3x2+…+anxn-1,则称数A可以表示成x进制形式,简记为:A=
.如:A=
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
(1)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,ak+1=
,k∈N*,bn=
(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(3)若常数t满足t≠0且t>-1,dn=
,求
.
查看习题详情和答案>>
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
(1)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,ak+1=
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
(3)若常数t满足t≠0且t>-1,dn=
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
对于定义在D上的函数y=f(x),若同时满足.
①存在闭区间[a,b]⊆D,使得任取x1∈[a,b],都有f(x1)=c (c是常数);
②对于D内任意x2,当x2∉[a,b]时总有f(x2)>c称f(x)为“平底型”函数.
(1)(理)判断f1(x)=|x-1|+|x-2|,f2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
,x∈[-2,+∞)是“平底型”函数,求m和n的值;
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件. 查看习题详情和答案>>
①存在闭区间[a,b]⊆D,使得任取x1∈[a,b],都有f(x1)=c (c是常数);
②对于D内任意x2,当x2∉[a,b]时总有f(x2)>c称f(x)为“平底型”函数.
(1)(理)判断f1(x)=|x-1|+|x-2|,f2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
| x2+2x+n |
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件. 查看习题详情和答案>>