摘要:(Ⅱ)设以原点为顶点.为焦点的抛物线为.若过点的直线与相交于不同.的两点..求线段的中点的轨迹方程.
网址:http://m.1010jiajiao.com/timu_id_182667[举报]
 ,
, ,
, 为常数,离心率为
为常数,离心率为 的双曲线
的双曲线 :
: 上的动点
上的动点 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为 ,抛物线
,抛物线 :
:
 的焦点与双曲线
的焦点与双曲线 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线 :
: (
( 为负常数)上任意一点
为负常数)上任意一点 向抛物线
向抛物线 引两条切线,切点分别为
引两条切线,切点分别为 、
、 ,坐标原点
,坐标原点 恒在以
恒在以 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
第二问中, 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得:
借助于根与系数的关系得到即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即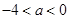
解:(Ⅰ)由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
(Ⅱ)设 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得: ,
,
即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即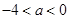
查看习题详情和答案>>
已知顶点在坐标原点,焦点在x轴正半轴的抛物线上有一点 ,A点到抛物线焦点的距离为1.
,A点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设M(x,y)为抛物线上的一个定点,过M作抛物线的两条互相垂直的弦MP,MQ,求证:PQ恒过定点(x+2,-y).
(3)直线x+my+1=0与抛物线交于E,F两点,在抛物线上是否存在点N,使得△NEF为以EF为斜边的直角三角形.
查看习题详情和答案>>
 ,A点到抛物线焦点的距离为1.
,A点到抛物线焦点的距离为1.(1)求该抛物线的方程;
(2)设M(x,y)为抛物线上的一个定点,过M作抛物线的两条互相垂直的弦MP,MQ,求证:PQ恒过定点(x+2,-y).
(3)直线x+my+1=0与抛物线交于E,F两点,在抛物线上是否存在点N,使得△NEF为以EF为斜边的直角三角形.
查看习题详情和答案>>
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|= .
.
(I)求曲线C1和C2的方程;
(II)设点C是C2上一点,若|CF1|=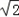 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
 ,|AF2|=
,|AF2|= .
.(I)求曲线C1和C2的方程;
(II)设点C是C2上一点,若|CF1|=
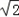 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.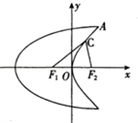
 ,|AF2|=
,|AF2|= .
.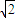 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.