题目内容
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|= .
.
(I)求曲线C1和C2的方程;
(II)设点C是C2上一点,若|CF1|=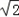 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
 ,|AF2|=
,|AF2|= .
.(I)求曲线C1和C2的方程;
(II)设点C是C2上一点,若|CF1|=
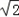 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.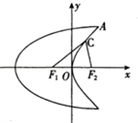
解:(I)设曲线C1的方程为 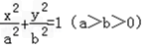 ,
,
则2a=|AF1|+|AF2|= 得a=3
得a=3
设A(x,y),F1(﹣c,0),F2(c,0),
则(x+c)2+y2=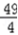 ,(x﹣c)2+y2=
,(x﹣c)2+y2= 
两式相减可得:xc=
由抛物线定义可知|AF2|=x+c= ∴c=1,x=
∴c=1,x= 或x=1,c=
或x=1,c=  (舍去)
(舍去)
所以曲线C1的方程为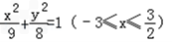 ,C2的方程为y2=4x(0≤x≤
,C2的方程为y2=4x(0≤x≤  );
);
(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,
依题意知l为抛物线C2的准线,则|CC1|=|CF2|
在直角△CC1F1中,|CF1|= |CC1|,∠C1CF1=45°
|CC1|,∠C1CF1=45°
∵∠CF1F2=∠C1CF1=45°
在△CF1F2中,设|CF2|=r,则|CF1|=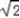 r,|F1F2|=2
r,|F1F2|=2
由余弦定理可得22+2r2﹣2×2×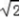 rcos45°=r2, ∴r=2
rcos45°=r2, ∴r=2
∴S△CF1F2=

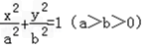 ,
,则2a=|AF1|+|AF2|=
 得a=3
得a=3设A(x,y),F1(﹣c,0),F2(c,0),
则(x+c)2+y2=
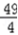 ,(x﹣c)2+y2=
,(x﹣c)2+y2= 
两式相减可得:xc=

由抛物线定义可知|AF2|=x+c=
 ∴c=1,x=
∴c=1,x= 或x=1,c=
或x=1,c=  (舍去)
(舍去)所以曲线C1的方程为
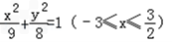 ,C2的方程为y2=4x(0≤x≤
,C2的方程为y2=4x(0≤x≤  );
);(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,
依题意知l为抛物线C2的准线,则|CC1|=|CF2|
在直角△CC1F1中,|CF1|=
 |CC1|,∠C1CF1=45°
|CC1|,∠C1CF1=45° ∵∠CF1F2=∠C1CF1=45°
在△CF1F2中,设|CF2|=r,则|CF1|=
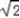 r,|F1F2|=2
r,|F1F2|=2 由余弦定理可得22+2r2﹣2×2×
 rcos45°=r2, ∴r=2
rcos45°=r2, ∴r=2 ∴S△CF1F2=



练习册系列答案
相关题目
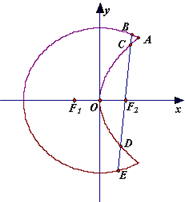 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=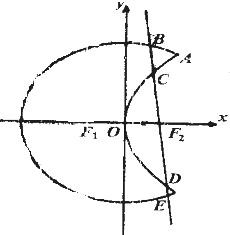 曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,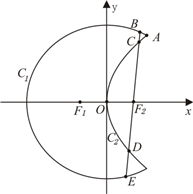 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= 如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,