摘要:(1)在中,令得
网址:http://m.1010jiajiao.com/timu_id_181974[举报]
在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m (m为正常数) 且
=m (m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求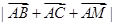 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求
为所求
第二问因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则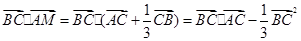 =
=
(2)当 时,则
时,则 =
=
第三问中,解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求……………2分
为所求……………2分
(Ⅱ)解:因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则 =
= ;-2分
;-2分
(2)当 时,则
时,则 =
= ;--2分
;--2分
(Ⅲ)解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令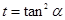 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
查看习题详情和答案>>
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
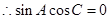

又由 得
得 即
即

又由 得
得 即
即

又
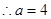 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

查看习题详情和答案>>
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义函数F(x)=
-1(0<x≤1),点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
的等比数列,O为原点,令
=
+
+…+
,是否存在点Q(1,m),使得
⊥
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
| 1 |
| 2 |
 在如图所示三角形中,令第n行的各数的和为an,得到数{an},则数列{an}的通项公式为
在如图所示三角形中,令第n行的各数的和为an,得到数{an},则数列{an}的通项公式为