题目内容
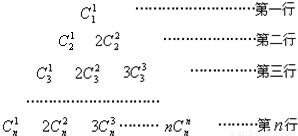
 在如图所示三角形中,令第n行的各数的和为an,得到数{an},则数列{an}的通项公式为
在如图所示三角形中,令第n行的各数的和为an,得到数{an},则数列{an}的通项公式为an=n•2n-1
an=n•2n-1
.分析:利用组合数的性质:k
=k
=n
对所求的式子进行化简,然后利用组合数的性质进行求解即可
| C | k n |
| n! |
| k!(n-k)! |
| (n-1)! |
| (k-1)![(n-1)-(k-1)]! |
解答:解:∵k
=k
=n
∴an=Cn1+2Cn2+…+nCnn
=n(Cn-10+Cn-11+Cn-12+…+Cn-1n-1)
=n•2n-1
故答案为:n•2n-1
| C | k n |
| n! |
| k!(n-k)! |
| (n-1)! |
| (k-1)![(n-1)-(k-1)]! |
∴an=Cn1+2Cn2+…+nCnn
=n(Cn-10+Cn-11+Cn-12+…+Cn-1n-1)
=n•2n-1
故答案为:n•2n-1
点评:本题主要考查了组合数的两个性质①kCnk=nCn-1k-1②Cn0+Cn1+…+Cnn=2n的应用,解题的关键是根据性质对所求的式子进行转化.

练习册系列答案
相关题目
 (2013•湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
(2013•湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
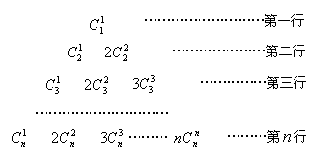 在如图所示三角形中,令第
在如图所示三角形中,令第