∴.即定点E的坐标为----------12分——青夏教育精英家教网——

摘要：∴.即定点E的坐标为----------12分

网址：http://m.1010jiajiao.com/timu_id_179989[举报]

已知点E、F的坐标分别是（-2，0）、（2，0），直线EP、FP相交于点P，且它们的斜率之积为-

．
（1）求证：点P的轨迹在一个椭圆C上，并写出椭圆C的方程；
（2）设过原点O的直线AB交（1）中的椭圆C于点A、B，定点M的坐标为(1，

)，试求△MAB面积的最大值，并求此时直线AB的斜率k_AB；
（3）反思（2）题的解答，当△MAB的面积取得最大值时，探索（2）题的结论中直线AB的斜率k_AB和OM所在直线的斜率k_OM之间的关系．由此推广到点M位置的一般情况或椭圆的一般情况（使第（2）题的结论成为推广后的一个特例），试提出一个猜想或设计一个问题，尝试研究解决．
[说明：本小题将根据你所提出的猜想或问题的质量分层评分]．

查看习题详情和答案>>

设m∈R，在平面直角坐标系中，已知向量

=（mx，y+1），向量

=（x，y-1），

，动点M（x，y）的轨迹为E．
（1）求轨迹E的方程，并说明该方程所表示曲线的形状；
（2）点P为当m=

时轨迹E上的任意一点，定点Q的坐标为（3，0），点N满足

，试求点N的轨迹方程．

查看习题详情和答案>>

（2012•浙江模拟）在直角坐标平面中，△ABC的两个顶点为A（0，-1），B（0，1）平面内两点G、M同时满足①

（1）求顶点C的轨迹E的方程
（2）设P、Q、R、N都在曲线E上，定点F的坐标为（

，0），已知

=0．求四边形PRQN面积S的最大值和最小值．

查看习题详情和答案>>

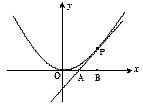如图，已知直线l与抛物线x²=4y相切于点P（2，1），且与x轴交于点A，定点B的坐标为（2，0）．
（I）若动点M满足

|=0，求点M的轨迹C；
（Ⅱ）若过点B的直线l′（斜率不等于零）与（I）中的轨迹C交于不同的两点E、F（E在B、F之间），试求△OBE与△OBF面积之比的取值范围．查看习题详情和答案>>

（2012•江西模拟）已知椭圆的两个焦点F1(-

，0)，过F₁且与坐标轴不平行的直线l₁与椭圆相交于M，N两点，△MNF₂的周长等于8．若过点（1，0）的直线l与椭圆交于不同两点P、Q，x轴上存在定点E（m，0），使

恒为定值，则E的坐标为（　　）

查看习题详情和答案>>