摘要:(Ⅱ)若.求证:是等比数列,
网址:http://m.1010jiajiao.com/timu_id_179912[举报]
等比数列{cn}满足cn+1+cn=5•22n-1,n∈N*,数列{an}满足an=log2cn
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
,Tn为数列{bn}的前n项和.求证:Tn<
;
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
查看习题详情和答案>>
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
设等比数列{an}的前n项的和为Sn,公比为q(q≠1).
(1)若S4,S12,S8成等差数列,求证:a10,a18,a14成等差数列;
(2)若Sm,Sk,St(m,k,t为互不相等的正整数)成等差数列,试问数列{an}中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若q为大于1的正整数.试问{an}中是否存在一项ak,使得ak恰好可以表示为该数列中连续两项的和?请说明理由.
查看习题详情和答案>>
(1)若S4,S12,S8成等差数列,求证:a10,a18,a14成等差数列;
(2)若Sm,Sk,St(m,k,t为互不相等的正整数)成等差数列,试问数列{an}中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若q为大于1的正整数.试问{an}中是否存在一项ak,使得ak恰好可以表示为该数列中连续两项的和?请说明理由.
设等比数列 的前n项和为Sn,已知
的前n项和为Sn,已知
(1)求数列 通项公式;
通项公式;
(2)在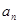 与
与 之间插入n个数,使这n+2个数组成一个公差为
之间插入n个数,使这n+2个数组成一个公差为 的等差数列。
的等差数列。
(Ⅰ)求证:
(Ⅱ)在数列 中是否存在三项
中是否存在三项 (其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
(其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
查看习题详情和答案>>
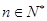 )
)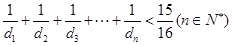 .
. )
)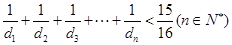 .
.