摘要:由①.②得: 故k的取值范围为 ---------12分
网址:http://m.1010jiajiao.com/timu_id_178824[举报]
已知f(n)=(2n+7)3n+9,存在自然数m,使得对任意正整数n,都能使m整除f(n),猜测出最大的m的值。并用数学归纳法证明你的猜测是正确的。
【解析】本试题主要考查了归纳猜想的运用,以及数学归纳法的证明。
∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除
然后证明n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1?-(2k+7)·3k=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2?(k≥2) 证明得到。解析 ∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除
证明 n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1?-(2k+7)·3k=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2?(k≥2)  f(k+1)能被36整除
f(k+1)能被36整除
∵f(1)不能被大于36的数整除,∴所求最大的m值等于36
查看习题详情和答案>>
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程
=
x+
必过(
,
);
④在一个2×2列联中,由计算得K2=13.079则有99%的把握确认这两个变量间有关系;
其中错误 的个数是( )
本题可以参考独立性检验临界值表:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
 |
| y |
③线性回归方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
④在一个2×2列联中,由计算得K2=13.079则有99%的把握确认这两个变量间有关系;
其中错误 的个数是( )
本题可以参考独立性检验临界值表:
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
| A、0 | B、1 | C、2 | D、3 |
下列四个命题中
①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“?x0∈R,x02-x0-1>0“的否定¬P:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-l<X<0)=
-p;
④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.
其中正确的命题的个数有( )
附:本题可以参考独立性检验临界值表
①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“?x0∈R,x02-x0-1>0“的否定¬P:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-l<X<0)=
| 1 |
| 2 |
④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.
其中正确的命题的个数有( )
附:本题可以参考独立性检验临界值表
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10. 828 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 满足
满足 ,试判定
,试判定 ,
,
 ,
, ,
, 是直角三角形.
是直角三角形.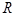 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于

 ,
,