摘要：函数的最小正周期为 . 三角函数的性质(2)[考纲要求]掌握三角函数的性质.[考试内容]正弦.余弦.正切.余切函数的性质.[复习建议]在熟练掌握基本三角函数性质的基础上.要善于把三角函数式尽可能转化为只含一个三角函数的“标准式 .进而取确定其性质.在确定三角函数的单调区间时.常可先分析函数的定义域和周期.画出大致图象后在通过观察得出结论.[知识回顾]函数奇偶性单调区间y=sinx 增区间: 减区间: y=cosx 增区间: 减区间: y=tanx 增区间:y=cotx 减区间:
网址：http://m.1010jiajiao.com/timu_id_177723[举报]
。
的最小正周期，并判断奇偶性；
的三个内角，若
，且C为锐角，求
。
。
的最小正周期，并判断奇偶性；
的三个内角，若
，且C为锐角，求
。已知函数
。
（1）求函数的最小正周期和最大值；
（2）求函数的增区间；
（3）函数的图象可以由函数
的图象经过怎样的变换得到？
【解析】本试题考查了三角函数的图像与性质的运用。第一问中，利用可知函数的周期为
，最大值为
。
第二问中，函数
的单调区间与函数
的单调区间相同。故当
，解得x的范围即为所求的区间。
第三问中，利用图像将的图象先向右平移
个单位长度，再把横坐标缩短为原来的
（纵坐标不变），然后把纵坐标伸长为原来的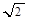
倍（横坐标不变），再向上平移1个单位即可。
解：（1）函数
的最小正周期为，最大值为。
（2）函数的单调区间与函数的单调区间相同。
即
所求的增区间为
，
即
所求的减区间为
，
。
（3）将的图象先向右平移个单位长度，再把横坐标缩短为原来的 （纵坐标不变），然后把纵坐标伸长为原来的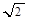倍（横坐标不变），再向上平移1个单位即可。
查看习题详情和答案>>
。
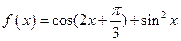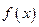的最小正周期,并判断奇偶性； 
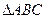的三个内角，若
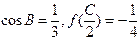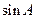，且C为锐角，求sinA。
。
的最小正周期,并判断奇偶性； 
的三个内角，若
，且C为锐角，求sinA。