摘要：的条件下P点的横坐标.点N在y轴上.且|PN|等于点P到直线的距离.圆M能覆盖三角形APN.当圆M的面积最小时.求圆M的方程.
网址：http://m.1010jiajiao.com/timu_id_163229[举报]
已知点P在曲线C：y＝
(x＞1)上，设曲线C在点P处的切线为l，若l与函数y＝kx(k＞0)的图像交于点A，与X轴相交于B点，设点P的横坐标为t，设A，B的横坐标分别为xA，xB，记f(t)＝xA·xB
(1)求函数f(t)的解析式
(2)设数列{an}(n≥1，n∈N)满足a1＝1，an＝f(
)(n≥2)，设数列{bn}(n≥1，n∈N，满足bn＝
－
，求{an}和{bn}的通项公式
(3)在(2)的条件下，当1＜k＜3时，证明不等式a1＋a2＋a3…＋an＞
．
己知函数f(x)=log3
，M(x1，y1)，N(x2，y2)是f（x）图象点的两点，横坐标为
的点P是M，N的中点．
（1）求证：y1+y2的定值；
（2）若Sn=f(
)+f(
)+…+f(
)(n∈N*，n≥2)，an=
(n∈N*)，Tn为数列{an}前n项和，当Tn＜m（Sn+1+1）对一切n∈N*都成立时，试求实数m的取值范围．
（3）在（2）的条件下，设bn=
，Bn为数列{bn}前n项和，证明：Bn＜
．
查看习题详情和答案>>
| ||
| 1-x |
| 1 |
| 2 |
（1）求证：y1+y2的定值；
（2）若Sn=f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
|
（3）在（2）的条件下，设bn=
| 1 |
| 4(Sn+1+1)(Sn+2+1)+1 |
| 17 |
| 52 |
已知f(x)=
(x∈R)，P1（x1，y1）、P2（x2，y2）是函数y=f（x）图象上两点，且线段P1P2中点P的横坐标是
．
（1）求证点P的纵坐标是定值；
（2）若数列{an}的通项公式是an=f(
)（m∈N*），n=1，2…m），求数列{an}的前m项和Sm；
（3）在（2）的条件下，若m∈N*时，不等式
＜
恒成立，求实数a的取值范围．
查看习题详情和答案>>
| 1 |
| 4x+2 |
| 1 |
| 2 |
（1）求证点P的纵坐标是定值；
（2）若数列{an}的通项公式是an=f(
| n |
| m |
（3）在（2）的条件下，若m∈N*时，不等式
| am |
| Sm |
| am+1 |
| Sm+1 |
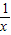（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
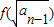（n≥2），数列{bn}满足bn=
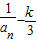，求an与bn；
．
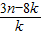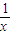（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
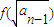（n≥2），数列{bn}满足bn=
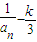，求an与bn；
．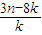