1．1   2．    3．    4．－8    5．   6．20         7．

8．1   9．0     10．    11．   12．     13．   14．（1005，1004）

15．⑴ ∵ ，………………… 2分

又∵ ，∴ 而为斜三角形，

∵，∴.   ……………………………………………… 4分

∵，∴ .  …………………………………… 6分

⑵∵，∴ …12分

即，∵，∴.…………………………………14分

16．⑴∵平面，平面，所以，…2分

∵是菱形，∴，又，

∴平面，……………………………………………………4分

又∵平面，∴平面平面．  …………………………6分

⑵取中点，连接,则，

∵是菱形，∴，

∵为的中点，∴，………………10分

∴．

∴四边形是平行四边形，∴，………………12分

又∵平面，平面．

∴平面．     ……………………………………14分

17．解：（1）依题意数列的通项公式是，

故等式即为，

同时有，

两式相减可得        …………………3分

可得数列的通项公式是，

知数列是首项为1，公比为2的等比数列。           ………6分

18．解：（Ⅰ）当9天购买一次时，该厂用于配料的保管费用

P=70+=88(元)             ……………4分 

   （Ⅱ）（1）当x≤7时

y=360x+10x+236=370x+236                        ………5分

        （2）当 x>7时

y=360x+236+70+6[()+()+……+2+1]  

              =                              ………7分

         ∴                      ………8分 

         ∴设该厂x天购买一次配料平均每天支付的费用为f(x)元

                    …………11分

当x≤7时

  当且仅当x=7时             

f(x)有最小值（元）

当x＞7时

=≥393           

    当且仅当x=12时取等号

∵393<404

∴当x=12时 f(x)有最小值393元                  ………16分

19．（1）∵直线过点，且与圆：相切，

设直线的方程为，即，　……………2分

则圆心到直线的距离为，解得，

∴直线的方程为，即．…………4分

（2）对于圆方程,令，得,即．又直线过点且与轴垂直，∴直线方程为，设，则直线方程为

解方程组,得同理可得,……… 10分

∴以为直径的圆的方程为，

又，∴整理得，………… 12分

若圆经过定点，只需令，从而有，解得，

∴圆总经过定点坐标为． ……………………… 14分

22．解：（Ⅰ），………………1分

又，

处的切线方程为

…………3分

（Ⅱ），

…………………………………………4分

令，

则上单调递增，

上存在唯一零点，上存在唯一的极值点………6分

取区间作为起始区间，用二分法逐次计算如下

区间中点坐标

中点对应导数值

取区间

1

0.6

0.3

由上表可知区间的长度为0.3，所以该区间的中点，到区间端点距离小于0.2，因此可作为误差不超过0.2的一个极值点的相应x的值。

取得极值时，相应………………………9分

（Ⅲ）由，

即，

，………………………………………12分

令

令

上单调递增，

，

因此上单调递增，

则，

的取值范围是………………………………………16分

数学附加题参考答案及评分标准

21A．证明：连结AC．                        

因为EA切于A， 所以∠EAB＝∠ACB．

因为，所以∠ACD＝∠ACB，AB＝AD．

于是∠EAB＝∠ACD． ……………………………………………4分

又四边形ABCD内接于，所以∠ABE＝∠D．

所以∽．

于是，即．

所以．              ……………………………10分

21B．解：设为曲线上的任意一点，在矩阵A变换下得到另一点，

则有，…………………………………4分

即   所以……………………………………………………8分

又因为点P在曲线上，所以，

故有  即所得曲线方程.………………………………………………… 10分

21C．解：将曲线的极坐标方程化为直角坐标方程为，

即，它表示以为圆心，2为半径的圆，      ………………………………4分

直线方程的普通方程为，                          ………………………………6分

圆C的圆心到直线l的距离，……………………………………………………………………8分

故直线被曲线截得的线段长度为．   ……………………………………10分

21D．解：由柯西不等式，得  

．   ………………………………10分

22．以点为坐标原点, 以分别为轴,建立如图空间直角坐标系, 不妨设 则

所以   

设平面的法向量为

选做题
A．选修4-2矩阵与变换
已知矩阵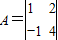，向量=．
（Ⅰ）求A的特征值λ₁、λ₂和特征向量α₁、α₂；   （Ⅱ）计算A⁶α的值．
B．选修4-4坐标系与参数方程
已知直线l的参数方程为（t为参数），P是椭圆上任意一点，求点P到直线l的距离的最大值．
查看习题详情和答案>>