题目内容
选做题A.选修4-2矩阵与变换
已知矩阵A=
|
| a |
|
(Ⅰ)求A的特征值λ1、λ2和特征向量α1、α2; (Ⅱ)计算A6α的值.
B.选修4-4坐标系与参数方程
已知直线l的参数方程为
|
| x2 |
| 4 |
分析:A:(I)本题考查矩阵的特征值及特征向量,先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
(II)对某个向量连续施行多次变化的计算;
B:将直线的参数方程化成普通方程为x+2y=0,并设椭圆上任一点P为(2cosθ,sinθ),则可根据点到直线的距离公式得到:P到直线l的距离是一个关于θ的函数,即可求解
(II)对某个向量连续施行多次变化的计算;
B:将直线的参数方程化成普通方程为x+2y=0,并设椭圆上任一点P为(2cosθ,sinθ),则可根据点到直线的距离公式得到:P到直线l的距离是一个关于θ的函数,即可求解
解答:A解:(Ⅰ)矩阵A的特征多项式为:f(λ)=
=λ2-5λ+6=0
得:λ1=2,λ2=3,当λ1=2时,解得α1=(2,1)
当λ2=3时,解得α2=(1,1).
(Ⅱ)由α=mα1+nα2
得
解得:
由(2)得:A5α=A5(3α1+α2)=3(A5α1)+A5α2=3(λ15α1)+λ25α2=3×25×(2,1)+35×(1,1)=(435,339)
B.坐标系与参数方程
解:直线l的参数方程为
(t为参数)故直线l的普通方程为x+2y=0
因为p为椭圆
+y2=1上任意点,故可设P(2cosθ,sinθ)其中θ∈R.
因此点P到直线l的距离是d=
=
所以当θ=kπ+
,k∈z时,d取得最大值
.
|
得:λ1=2,λ2=3,当λ1=2时,解得α1=(2,1)
当λ2=3时,解得α2=(1,1).
(Ⅱ)由α=mα1+nα2
得
|
解得:
|
由(2)得:A5α=A5(3α1+α2)=3(A5α1)+A5α2=3(λ15α1)+λ25α2=3×25×(2,1)+35×(1,1)=(435,339)
B.坐标系与参数方程
解:直线l的参数方程为
|
因为p为椭圆
| x2 |
| 4 |
因此点P到直线l的距离是d=
| |2cosθ+2sinθ| | ||
|
2
| ||||
|
所以当θ=kπ+
| π |
| 4 |
2
| ||
| 5 |
点评:本题考查了二阶矩阵,直线的参数方程,直线与圆锥曲线的综合问题属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
二阶矩阵
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
;C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为??=l与??=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数
 的最大值.
的最大值.  (2012•江苏二模)选做题
(2012•江苏二模)选做题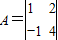 ,向量
,向量 =
= .
. (t为参数),P是椭圆
(t为参数),P是椭圆 上任意一点,求点P到直线l的距离的最大值.
上任意一点,求点P到直线l的距离的最大值.