��Ŀ����
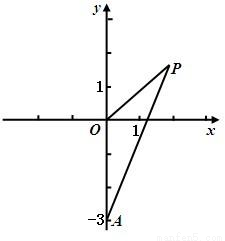
 ��ͼ����֪��A��0��-3��������P����|PA|=2|PO|������OΪ����ԭ�㣮
��ͼ����֪��A��0��-3��������P����|PA|=2|PO|������OΪ����ԭ�㣮������P�Ĺ켣���̣�
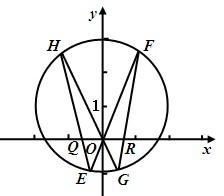
���ǣ��������õ�����ΪC����ԭ��O������ֱ��l1��y=k1x��l2��y=k2x�ֱ�����C�ڵ�E��x1��y1����F��x2��y2����G��x3��y3����H��x4��y4��������y2��0��y4��0������֤��
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
��III�����ڣ����е�E��F��G��H����EH��x���ڵ�Q��GF��x���ڵ�R����֤��|OQ|=|OR|����֤�����̲�����EH��GF��ֱ��x������Σ�
��������1�����P������Ϊ��x��y����������ʾ��|PA|��|PO|������|PA|=2|PO|����ĵ�P�Ĺ켣���̣�
��2����ֱ��EF��GH�ķ��̷ֱ����ԲC���̣�����Τ�ﶨ���ֱ���ý��������֮����֮������������
��
��֤��ԭʽ��
��3�����Q��q��0������Q��r��0������E��Q��H���㹲�����q�ı���ʽ������F��R��G���㹲�����r�ı���ʽ���������ݣ�2���е�
=
������
+
=0��������֪q+r=0������|q|=|r|����|OQ|=|OR|��
��2����ֱ��EF��GH�ķ��̷ֱ����ԲC���̣�����Τ�ﶨ���ֱ���ý��������֮����֮������������
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
��3�����Q��q��0������Q��r��0������E��Q��H���㹲�����q�ı���ʽ������F��R��G���㹲�����r�ı���ʽ���������ݣ�2���е�
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| (k1-k2)x2x3 |
| k1x2-k2x3 |
| (k1-k2)x1x4 |
| k1x1-k2x4 |
��� �⣺�������P��x��y����������ɵ�
�⣺�������P��x��y����������ɵ�
=2
������x2+y2-2y-3=0
�ʶ���P�Ĺ켣����Ϊx2+y2-2y-3=0��
����ֱ��EF�ķ���y=k1x����ԲC����
�����ã�k12+1��x2-2k1x-3=0
���ݸ���ϵ���Ĺ�ϵ��x1+x2=
��x1x2=-
��
��ֱ��GH�ķ���y=k2x����ԲC���̣�
ͬ���ɵ�x3+x4=
��x3x4=-
��
�ɢ١��ڿɵ�
=-
=
�����Խ��۳�����
�������Q��q��0������Q��r��0������E��Q��H���㹲��
��
=
�����q=
��F��R��G���㹲��
ͬ���ɵ�r=
��
=
���ε�
=
��
+
=0��
�Ӷ�q+r=0������|q|=|r|����|OQ|=|OR|��
 �⣺�������P��x��y����������ɵ�
�⣺�������P��x��y����������ɵ�| x2+(y+3)2 |
| x2+y2 |
������x2+y2-2y-3=0
�ʶ���P�Ĺ켣����Ϊx2+y2-2y-3=0��
����ֱ��EF�ķ���y=k1x����ԲC����
�����ã�k12+1��x2-2k1x-3=0
���ݸ���ϵ���Ĺ�ϵ��x1+x2=
| 2k1 |
| k12+1 |
| 3 |
| k12+1 |
��ֱ��GH�ķ���y=k2x����ԲC���̣�
ͬ���ɵ�x3+x4=
| 2k2 |
| k22+1 |
| 3 |
| k22+1 |
�ɢ١��ڿɵ�
| k1x1x2 |
| x1+x2 |
| 3 |
| 2 |
| k2x3x4 |
| x3+x4 |
�������Q��q��0������Q��r��0������E��Q��H���㹲��
��
| x1-q |
| k1x1 |
| x4-q |
| k2x4 |
| (k1-k2)x1x4 |
| k1x1-k2x4 |
��F��R��G���㹲��
ͬ���ɵ�r=
| (k1-k2)x2x3 |
| k1x2-k2x3 |
��
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| x2x3 |
| k1x2-k2x3 |
| -x1x4 |
| k1x1-k2x4 |
��
| (k1-k2)x2x3 |
| k1x2-k2x3 |
| (k1-k2)x1x4 |
| k1x1-k2x4 |
�Ӷ�q+r=0������|q|=|r|����|OQ|=|OR|��
������������Ҫ������Բ���̵��ۺ�Ӧ�ã��漰ֱ����Բ�Ĺ�ϵ����Ҫ��ֱ�߷�����Բ��������������Τ�ﶨ����������⣮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����֪��A��0��2����������y2=x+4������B��C��ʹ��AB��BC�����C���������ȡֵ��Χ��
��ͼ����֪��A��0��2����������y2=x+4������B��C��ʹ��AB��BC�����C���������ȡֵ��Χ��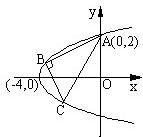
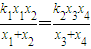 ��
��
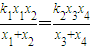 ��
��