摘要:分析 本题考查当n→∞时数列的极限.解题的关键是把结论中通项的比值用条件中前n项和的比值表示出来,即把转化成关于n的多项式.解法一 设Sn=kn?2n,Tn=kn.由an=Sn-Sn-1,得an=2kn2-2k(n-1)2=4kn-2k,bn=kn+1]=6kn-2k.
网址:http://m.1010jiajiao.com/timu_id_15757[举报]
已知{an}是各项均为正数的等差数列,lga1、lga2、lga4成等差数列.又bn=
,n=1,2,3,….
(Ⅰ)证明{bn}为等比数列;
(Ⅱ)如果无穷等比数列{bn}各项的和S=
,求数列{an}的首项a1和公差d.
(注:无穷数列各项的和即当n→∞时数列前项和的极限) 查看习题详情和答案>>
| 1 |
| a2n |
(Ⅰ)证明{bn}为等比数列;
(Ⅱ)如果无穷等比数列{bn}各项的和S=
| 1 |
| 3 |
(注:无穷数列各项的和即当n→∞时数列前项和的极限) 查看习题详情和答案>>
设m,n是空间两条不同直线,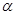 ,
, 是空间两个不同平面,则下列选项中不正确的是( )
是空间两个不同平面,则下列选项中不正确的是( )
(A)当n⊥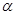 时,“n⊥
时,“n⊥ ”是“
”是“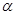 ∥
∥ ”成立的充要条件
”成立的充要条件
(B)当 时,“m⊥
时,“m⊥ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
(C)当 时,“n//
时,“n//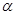 ”是“
”是“ ”必要不充分条件
”必要不充分条件
(D)当 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
查看习题详情和答案>>
已知下列命题:
①若当x→+∞时函数f(x)存在极限,则当n→∞时数列{f(n)}也存在极限;
②已知Sn=![]() +
+![]() +
+![]() +…+
+…+![]() ,则
,则![]() Sn=0+0+…+0=0;
Sn=0+0+…+0=0;
③若函数f(x)在点x=x0处的左、右极限都存在,且左、右极限值都等于a,则f(x0)=a;
④若f(x0)=a,则![]() f(x)=a.
f(x)=a.
其中正确命题的序号是__________________.
查看习题详情和答案>>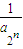 ,n=1,2,3,….
,n=1,2,3,…. ,求数列{an}的首项a1和公差d.
,求数列{an}的首项a1和公差d.