摘要:分析 本题考查正态总体N(μ,σ2)在任一区间(x1,x2)内取值的概率.解题的关键是根据公式F(x)=Φ(),把它化成标准正态总体N(0,1)来求解.
网址:http://m.1010jiajiao.com/timu_id_15506[举报]
设任一正态总体N(μ,σ2)中取值小于x的概率为F(x),标准正态总体N(0,1)中,取值小于x0 的概率为Φ(x0).
(1)证明F(x)可化为Φ(x0)计算.
(2)利用正态曲线的性质说明:当x取何值时,正态总体N(μ,σ2)相应的函数f(x)=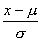 (x∈R)有最大值,其最大值是多少?
(x∈R)有最大值,其最大值是多少?
查标准正态分布得Φ(0.96)=0.831 5,Φ(1.81)=0.964 8,Φ(0.5)=0.691 5,Φ(2)=0.977 2,则标准正态总体落在区间(-1.81,0.96)内取值的概率为__________;正态总体N(2,1)落在区间(0,2.5)内取值的概率为__________.
查看习题详情和答案>>
已知一个总体呈正态分布N(μ,σ2),其总体密度函数是f(x)=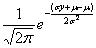
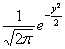 ,x∈R.
,x∈R.
(1)令y=![]() ,求证:F(y)=f(σy+μ)=
,求证:F(y)=f(σy+μ)=![]()
![]() (y∈R);
(y∈R);
(2)求正态总体N(2,4)在区间(-6,10)内的概率〔已知Φ(2)=0.977 2〕.
查看习题详情和答案>>