题目内容
一批灯泡的使用时间ξ(单位:小时)服从正态分布N(10 000,4002).(1)求这批灯泡中“使用时间超过10 800小时”的灯泡的概率;
(2)现从这批灯泡中随机抽取100个,求这100个灯泡中“使用时间超过10 800小时”的灯泡个数的期望.(下列数据供计算时选用:Φ(0.5)=0.691 5,Φ(1)=0.841 3,Φ(2)=0.977 2)
分析:本题考查正态分布与标准正态分布的转化及二项分布的数学期望.
解:(1)由已知μ=10 000,σ=400,设η&N(0,1),
则P(ξ>10 800)=P(η>![]() )=P(η>2)=1-Φ(2)=1-0.977 2=0.022 8,
)=P(η>2)=1-Φ(2)=1-0.977 2=0.022 8,
即这批灯泡中“使用时间超过10 800小时”的灯泡的概率为0.022 8.
(2)这100个灯泡中使用时间超过10 800小时的灯泡个数ξ是一个随机变量,且ξ&B(100,0.022 8),
∴Eξ=100×0.022 8=2.28,
即这100个灯泡中使用时间超过10 800小时的灯泡个数的期望为2.28.
点评:在标准正态总体N(0,1)中,相应于x0的值Φ(x0)是指总体小于x0的概率,即Φ(x0)=P(x<x0).对一般正态总体N(μ,σ2),在某一区间内取值的概率,均可依据公式![]() 转化成标准正态总体N(0,1)来进行研究.
转化成标准正态总体N(0,1)来进行研究.

练习册系列答案
相关题目
一批电池的使用时间X(单位:小时)服从正态分布N(36,42),在这批灯泡中任取一个“使用时间不小于40小时”的概率是( )
| A、0.9544 | B、0.6826 | C、0.3174 | D、0.1587 |
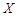 (单位:小时)服从正态分布
(单位:小时)服从正态分布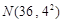 ,在这批灯泡中任取一个“使用时间不小于40小时”的概率是
,在这批灯泡中任取一个“使用时间不小于40小时”的概率是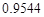 (B)
(B) (C)
(C) (D)
(D)