题目内容
设任一正态总体N(μ,σ2)中取值小于x的概率为F(x),标准正态总体N(0,1)中,取值小于x0 的概率为Φ(x0).(1)证明F(x)可化为Φ(x0)计算.
(2)利用正态曲线的性质说明:当x取何值时,正态总体N(μ,σ2)相应的函数f(x)=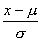
(x∈R)有最大值,其最大值是多少？
(1)证明:由正态总体N(μ,σ)的概率密度函数可知F(x)=Φ(),即x0=
.
(2)解析：由正态曲线的单调性和对称性可知,正态总体N(μ,σ2)的概率密度函数f(x)在x=μ时,取到最大值
.
练习册系列答案
相关题目
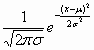(x∈R)有最大值，其最大值是多少？