摘要:分析 由式子an=5Sn-3,易得到an与Sn的关系式.由an=Sn-Sn-1,利用此式,再对n进行合适的赋值,便可消去Sn,得到{an}的递推关系式,进而确定数列{an},再求(a1+a3+a5+-+a2n-1).解 a1=S1,an=Sn-Sn-1.又已知an=5Sn-3,∴an-1=5Sn-1-3.两式相减,得an-an-1=5(Sn-Sn-1)=5an.
网址:http://m.1010jiajiao.com/timu_id_15368[举报]
已知f(x)=
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
=f(n)(n∈N+).
(1)若g(n)=
,求g(n)的最大值;
(2)若a1=
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
(3)若a1=
,数列{bn}的公差为3,且dn=bn-(n-1),h(x)=
.试证明:h(d1)•h(d2)…h(dn)<
.
查看习题详情和答案>>
| ax+1 |
| 3x-1 |
| Sn |
| Tn |
(1)若g(n)=
| an |
| bn |
(2)若a1=
| 5 |
| 2 |
(3)若a1=
| 5 |
| 2 |
| x |
| x+1 |
| 1 | ||
|
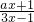 ,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且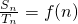 (n∈N+).
(n∈N+). ,求g(n)的最大值;
,求g(n)的最大值; ,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由. .试证明:h(d1)•h(d2)…h(dn)<
.试证明:h(d1)•h(d2)…h(dn)<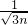 .
.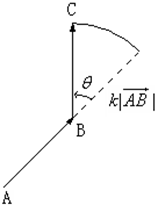 如图,
如图, 的大小是
的大小是 大小的k倍,
大小的k倍,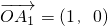
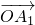 经过2次
经过2次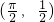 延伸,分别得到向量
延伸,分别得到向量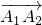 、
、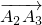 ,求
,求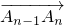 ,(n∈N*,n>1),设点An(xn,yn),求An的极限位置
,(n∈N*,n>1),设点An(xn,yn),求An的极限位置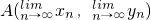
 ,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且 (n∈N+).
(n∈N+). ,求g(n)的最大值;
,求g(n)的最大值; ,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由. ,数列{bn}的公差为3,且dn=bn-(n-1),h(x)=
,数列{bn}的公差为3,且dn=bn-(n-1),h(x)= .试证明:h(d1)•h(d2)…h(dn)<
.试证明:h(d1)•h(d2)…h(dn)< .
. (2013•松江区二模)如图所示,向量
(2013•松江区二模)如图所示,向量