题目内容
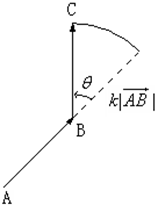 如图,
如图, 的大小是
的大小是 大小的k倍,
大小的k倍, 的方向由
的方向由 的方向逆时针旋转θ角得到,则我们称
的方向逆时针旋转θ角得到,则我们称 经过一次(θ,k)延伸得到
经过一次(θ,k)延伸得到 . 已知
. 已知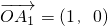
(1)向量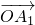 经过2次
经过2次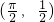 延伸,分别得到向量
延伸,分别得到向量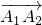 、
、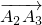 ,求
,求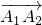 、
、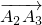 的坐标.
的坐标.
(2)向量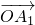 经过n-1次
经过n-1次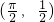 延伸得到的最后一个向量
延伸得到的最后一个向量
为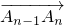 ,(n∈N*,n>1),设点An(xn,yn),求An的极限位置
,(n∈N*,n>1),设点An(xn,yn),求An的极限位置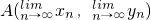
(3)向量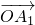 经过2次(θ,k)延伸得到向量
经过2次(θ,k)延伸得到向量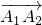 、
、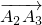 ,其中k>0,θ∈(0,π),若
,其中k>0,θ∈(0,π),若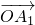 、
、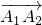 、
、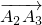 恰能够构成一个三角形(即A3与O重合),求θ,k的值.
恰能够构成一个三角形(即A3与O重合),求θ,k的值.
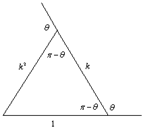 解:(1)
解:(1)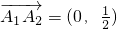 ,
,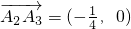
(2)
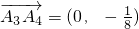 ,
,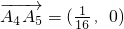 ,
,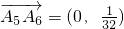 ,…
,…因为
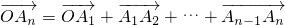
所以
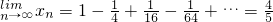 ,
,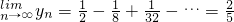
所以,A
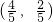
(3)
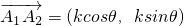 ,
,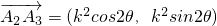
又∵
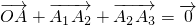
∴(1+kcosθ+k2cos2θ,ksinθ+k2sin2θ)=(0,0)
∴
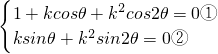
解得:k=1,θ=120°
分析:(1)向量
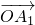 经过1次
经过1次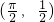 延伸,得到向量
延伸,得到向量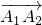 所在有向线段正向与y轴正向相同,且模为
所在有向线段正向与y轴正向相同,且模为 ,A2(1,
,A2(1, ),
),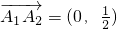 ,类似的,求出
,类似的,求出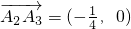
(2)
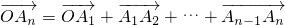 ,利用向量运算求出表达式,得出xn,yn再求极限.
,利用向量运算求出表达式,得出xn,yn再求极限.(3)若
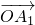 、
、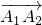 、
、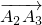 恰能够构成一个三角形,即
恰能够构成一个三角形,即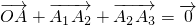 ,建立关于的方程组,再解方程组即可.
,建立关于的方程组,再解方程组即可.点评:本题是新定义题目,首先读懂新定义的实质,转化成我们已有的知识并解决.本题实质考查向量的坐标运算,几何运算,极限运算,方程的思想.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
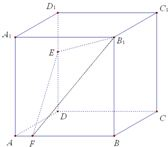 8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )
8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )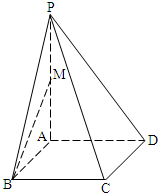 (2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.
(2008•嘉定区一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.
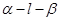 的大小是60°,线段
的大小是60°,线段 ,
,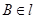 ,与
,与 所成的角为30°,则
所成的角为30°,则 与平面
与平面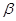 所成的角的正弦值是_________.
所成的角的正弦值是_________.