摘要:即(k+3)ak+1=a1+a2+-+ak-1+ak=ak+ak
网址:http://m.1010jiajiao.com/timu_id_15362[举报]
设Tn为数列{an}的前n项的积,即Tn=a1•a2…an.
(1)若Tn=n2,求a3a4a5的值;
(2)若数列{an}各项都是正数,且满足Tn=
((n∈N*),证明数列{log2an}为等比数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:①a1•a2…a100=2;②等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立.试问符合条件的数列共有多少个?为什么?
查看习题详情和答案>>
(1)若Tn=n2,求a3a4a5的值;
(2)若数列{an}各项都是正数,且满足Tn=
| ||
| 4 |
(3)数列{an}共有100项,且满足以下条件:①a1•a2…a100=2;②等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立.试问符合条件的数列共有多少个?为什么?
对于项数为m的有穷数列{an},记bk=max{a1,a2,…,ak}(k=1,2,…,m),即bk为a1,a2,…,ak中的最大值,并称数列{bn}是{an}的控制数列,如1,3,2,5,5的控制数列是1,3,3,5,5。
(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an}。
(2)设{bn}是{an}的控制数列,满足ak+bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m)。
(3)设m=100,常数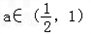 ,若
,若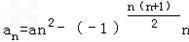 ,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100)。
,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100)。
查看习题详情和答案>>
(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an}。
(2)设{bn}是{an}的控制数列,满足ak+bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m)。
(3)设m=100,常数
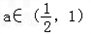 ,若
,若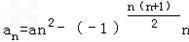 ,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100)。
,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100)。
对于项数为m的有穷数列{an},记bk=max{a1,a2,…,ak}(k=1,2,…,m),即bk为a1,a2,…,ak中的最大值,并称数列{bn}是{an}的控制数列,如1,3,2,5,5的控制数列是1,3,3,5,5.
(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an}.
(2)设{bn}是{an}的控制数列,满足ak+bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m).
(3)设m=100,常数 ,若
,若 ,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
查看习题详情和答案>>
(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an}.
(2)设{bn}是{an}的控制数列,满足ak+bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m).
(3)设m=100,常数
 ,若
,若 ,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).查看习题详情和答案>>