题目内容
设Tn为数列{an}的前n项的积,即Tn=a1•a2…an.
(1)若Tn=n2,求a3a4a5的值;
(2)若数列{an}各项都是正数,且满足Tn=
((n∈N*),证明数列{log2an}为等比数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:①a1•a2…a100=2;②等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立.试问符合条件的数列共有多少个?为什么?
(1)若Tn=n2,求a3a4a5的值;
(2)若数列{an}各项都是正数,且满足Tn=
| ||
| 4 |
(3)数列{an}共有100项,且满足以下条件:①a1•a2…a100=2;②等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立.试问符合条件的数列共有多少个?为什么?
分析:(1)由Tn=a1•a2…an=n2,知a3a4a5=
,由此能求出a3a4a5的值.
(2)当n=1时,a1=4,log2a1=2,当n≥2时,an=
=
,由此能够证明数列{log2an}为等比数列,并求{an}的通项公式.
(3)由a1•a2…a100=2,等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立,知a1+
=3,解得a1=1,或a1=2.Tk是方程x2-(k+2)x+2=0的一个实根,当数列前k(2≤k≤98)项确定后,其前k项积Tk确定,由此能求出符合条件的数列的个数.
| T5 |
| T2 |
(2)当n=1时,a1=4,log2a1=2,当n≥2时,an=
| Tn |
| Tn-1 |
| an2 |
| an-12 |
(3)由a1•a2…a100=2,等式a1•a2…ak+ak+1•ak+2…a100=k+2对1≤k≤99,k∈N*恒成立,知a1+
| 2 |
| a1 |
解答:解:(1)∵Tn=a1•a2…an=n2,
∴a3a4a5=
=
.
(2)当n=1时,a1=T1=
,
∴a1=4,log2a1=2,
当n≥2时,an=
=
,
∵an>0,∴an=an-12,
∴log2an=2log2an-1,
∴数列{log2an}为等比数列,
logaan=2n,∴an=22n.
(3)∵a1×a2×…×a100=2;
等式a1•a2…ak+ak+1•ak+2…a100=3对1≤k≤99,k∈N*恒成立,
∴a1+a2•a3×…×a100=k+2,
∴a1+
=3,解得a1=1,或a1=2.
Tk是方程x2-(k+2)x+2=0的一个实根,
△=[-(k+2)]2-4=k2+4k>0,
当数列前k(2≤k≤98)项确定后,
其前k项积Tk确定,
由Tk+1可得到两个ak+1,
所以符合条件的数列共有299个.
∴a3a4a5=
| T5 |
| T2 |
| 25 |
| 4 |
(2)当n=1时,a1=T1=
| a12 |
| 4 |
∴a1=4,log2a1=2,
当n≥2时,an=
| Tn |
| Tn-1 |
| an2 |
| an-12 |
∵an>0,∴an=an-12,
∴log2an=2log2an-1,
∴数列{log2an}为等比数列,
logaan=2n,∴an=22n.
(3)∵a1×a2×…×a100=2;
等式a1•a2…ak+ak+1•ak+2…a100=3对1≤k≤99,k∈N*恒成立,
∴a1+a2•a3×…×a100=k+2,
∴a1+
| 2 |
| a1 |
Tk是方程x2-(k+2)x+2=0的一个实根,
△=[-(k+2)]2-4=k2+4k>0,
当数列前k(2≤k≤98)项确定后,
其前k项积Tk确定,
由Tk+1可得到两个ak+1,
所以符合条件的数列共有299个.
点评:本题考查等比数列的证明,考查数列的通项公式的求法,考查符合条件的数列个数的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
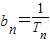 ,证明数列{bn}是等差数列,并求bn和an;
,证明数列{bn}是等差数列,并求bn和an; <Sn≤an-
<Sn≤an- .
.