题目内容
对于项数为m的有穷数列{an},记bk=max{a1,a2,…,ak}(k=1,2,…,m),即bk为a1,a2,…,ak中的最大值,并称数列{bn}是{an}的控制数列,如1,3,2,5,5的控制数列是1,3,3,5,5.(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an}.
(2)设{bn}是{an}的控制数列,满足ak+bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m).
(3)设m=100,常数
 ,若
,若 ,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
【答案】分析:(1)根据题意,可得数列{an}为:2,3,4,5,1;2,3,4,5,2;2,3,4,5,3;2,3,4,5,4,;2,3,4,5,5;
(2)依题意可得bk+1≥bk,又ak+bm-k+1=C,ak+1+bm-k=C,从而可得ak+1-ak=bm-k+1-bm-k≥0,整理即证得结论;
(3)根据 ,可发现,a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,通过比较大小,可得a4k-2>a4k-1,a4k>a4k-2,而a4k+1>a4k,a4k-1-a4k-2=(a-1)(8k-3),从而可求得(b1-a1)+(b2-a2)+…+(b100-a100)=(a2-a3)+(a6-a7)+…+(a98-a99)=
,可发现,a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,通过比较大小,可得a4k-2>a4k-1,a4k>a4k-2,而a4k+1>a4k,a4k-1-a4k-2=(a-1)(8k-3),从而可求得(b1-a1)+(b2-a2)+…+(b100-a100)=(a2-a3)+(a6-a7)+…+(a98-a99)= (a4k-2-a4k-1)=2525(1-a).
(a4k-2-a4k-1)=2525(1-a).
解答:解:(1)数列{an}为:2,3,4,5,1;2,3,4,5,2;2,3,4,5,3;2,3,4,5,4,;2,3,4,5,5;…4分
(2)∵bk=max{a1,a2,…,ak},bk+1=max{a1,a2,…,ak+1},
∴bk+1≥bk…6分
∵ak+bm-k+1=C,ak+1+bm-k=C,
∴ak+1-ak=bm-k+1-bm-k≥0,即ak+1≥ak,…8分
∴bk=ak…10分
(3)对k=1,2,…25,
a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),
a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,…12分
比较大小,可得a4k-2>a4k-1,
∵ <a<1,
<a<1,
∴a4k-1-a4k-2=(a-1)(8k-3)<0,即a4k-2>a4k-1;
a4k-a4k-2=2(2a-1)(4k-1)>0,即a4k>a4k-2,
又a4k+1>a4k,
从而b4k-3=a4k-3,b4k-2=a4k-2,b4k-1=a4k-2,b4k=a4k,…15分
∴(b1-a1)+(b2-a2)+…+(b100-a100)
=(a2-a3)+(a6-a7)+…+(a98-a99)
= (a4k-2-a4k-1)
(a4k-2-a4k-1)
=(1-a) (8k-3)
(8k-3)
=2525(1-a)…18分
点评:本题考查数列的应用,着重考查分析,对抽象概念的理解与综合应用的能力,对(3)观察,分析寻找规律是难点,是难题.
(2)依题意可得bk+1≥bk,又ak+bm-k+1=C,ak+1+bm-k=C,从而可得ak+1-ak=bm-k+1-bm-k≥0,整理即证得结论;
(3)根据
 ,可发现,a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,通过比较大小,可得a4k-2>a4k-1,a4k>a4k-2,而a4k+1>a4k,a4k-1-a4k-2=(a-1)(8k-3),从而可求得(b1-a1)+(b2-a2)+…+(b100-a100)=(a2-a3)+(a6-a7)+…+(a98-a99)=
,可发现,a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,通过比较大小,可得a4k-2>a4k-1,a4k>a4k-2,而a4k+1>a4k,a4k-1-a4k-2=(a-1)(8k-3),从而可求得(b1-a1)+(b2-a2)+…+(b100-a100)=(a2-a3)+(a6-a7)+…+(a98-a99)= (a4k-2-a4k-1)=2525(1-a).
(a4k-2-a4k-1)=2525(1-a).解答:解:(1)数列{an}为:2,3,4,5,1;2,3,4,5,2;2,3,4,5,3;2,3,4,5,4,;2,3,4,5,5;…4分
(2)∵bk=max{a1,a2,…,ak},bk+1=max{a1,a2,…,ak+1},
∴bk+1≥bk…6分
∵ak+bm-k+1=C,ak+1+bm-k=C,
∴ak+1-ak=bm-k+1-bm-k≥0,即ak+1≥ak,…8分
∴bk=ak…10分
(3)对k=1,2,…25,
a4k-3=a(4k-3)2+(4k-3),a4k-2=a(4k-2)2+(4k-2),
a4k-1=a(4k-1)2-(4k-1),a4k=a(4k)2-4k,…12分
比较大小,可得a4k-2>a4k-1,
∵
 <a<1,
<a<1,∴a4k-1-a4k-2=(a-1)(8k-3)<0,即a4k-2>a4k-1;
a4k-a4k-2=2(2a-1)(4k-1)>0,即a4k>a4k-2,
又a4k+1>a4k,
从而b4k-3=a4k-3,b4k-2=a4k-2,b4k-1=a4k-2,b4k=a4k,…15分
∴(b1-a1)+(b2-a2)+…+(b100-a100)
=(a2-a3)+(a6-a7)+…+(a98-a99)
=
 (a4k-2-a4k-1)
(a4k-2-a4k-1)=(1-a)
 (8k-3)
(8k-3)=2525(1-a)…18分
点评:本题考查数列的应用,着重考查分析,对抽象概念的理解与综合应用的能力,对(3)观察,分析寻找规律是难点,是难题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
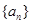 ,记
,记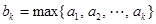 (k=1,2,…,m),即
(k=1,2,…,m),即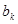 为
为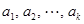 中的最大值,并称数列
中的最大值,并称数列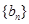 是
是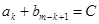 (C为常数,k=1,2,…,m).
(C为常数,k=1,2,…,m).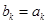 (k=1,2,…,m);(6分)
(k=1,2,…,m);(6分)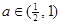 .若
.若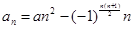 ,
,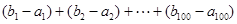 .
.