网址:http://m.1010jiajiao.com/timu_id_153090[举报]
一、选择题: DCABC CBBAC
二、填空题:11、卷.files/image183.gif) ; 12、23; 13、2; 14、4π; 15、
; 12、23; 13、2; 14、4π; 15、卷.files/image185.gif)
三、解答题:
16、解 (1)卷.files/image187.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 1分
1分
卷.files/image191.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 2分
2分
由已知有卷.files/image193.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 4分
4分
卷.files/image195.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 6分
6分
(2)卷.files/image197.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 10分
10分
= 卷.files/image199.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 11分
11分
= 卷.files/image201.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 12分
12分
17、解:(1)设红球有卷.files/image057.gif) 个,白球
个,白球卷.files/image204.gif) 个,依题意得
个,依题意得 卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 1分
1分
卷.files/image206.gif) ,
, 卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 3分
3分
解得卷.files/image208.gif)
故红球有6个.
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 5分
5分
(2)记“甲取出的球的编号大”为事件A,
所有的基本事件有:(1,2),(l,3),(1,4),
(2,1),(2,3),(2,4),
(3,1),(3,2),(3,4),
(4,1),(4,2),(4,3),
共12个基本事件 卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 8分
8分
事件A包含的基本事件有:(1,2),(1,3),(1,4)(2,1),
(2,3),(3,1),(3,2)(4,1),
共8个基本事件
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 11分
11分
所以,. 卷.files/image210.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif)
卷.files/image189.gif) 12分
12分
18、解:(1)底面三边长AC=3,BC=4,AB=5,
∠ACB=90°,∴ AC⊥BC, (2分)
又在直三棱柱ABC-A1B卷.files/image212.gif) 底面ABC,∴CC1⊥AC,(3分)
底面ABC,∴CC1⊥AC,(3分)
BC、CC1卷.files/image212.gif) 平面BCC1,且BC
与CC1相交
平面BCC1,且BC
与CC1相交
∴ AC⊥平面BCC1; (5分)
而BC1卷.files/image212.gif) 平面BCC1
平面BCC1
∴ AC⊥BC1 (6分)
(2)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,
∴ DE//AC1, (8分)
∵
DE卷.files/image212.gif) 平面CDB1,AC1
平面CDB1,AC1卷.files/image216.gif) 平面CDB1,
平面CDB1,
∴ AC1//平面CDB1;(10分)
(3)卷.files/image218.gif) (11分)
(11分)
=卷.files/image220.gif) -
-卷.files/image222.gif) (13分)
(13分)
=20 (14分)
19、解:(1)设椭圆的半长轴长、半短轴长、半焦距分别为a,b,c,则有
卷.files/image224.gif) ,
,卷.files/image226.gif)
由椭圆定义,有卷.files/image228.gif) ………1分
………1分
卷.files/image143.gif) =
=卷.files/image231.gif) ……………………………2分
……………………………2分
=卷.files/image233.gif) ……………………3分
……………………3分
≥卷.files/image235.gif) …………………………………………5分
…………………………………………5分
=卷.files/image237.gif) =
=卷.files/image239.gif) ……………………………………………6分
……………………………………………6分
∴卷.files/image143.gif) 的最小值为
的最小值为卷.files/image239.gif) 。
。
(当且仅当卷.files/image242.gif) 时,即
时,即卷.files/image141.gif) 取椭圆上下顶点时,
取椭圆上下顶点时,卷.files/image143.gif) 取得最小值 )……………7分
取得最小值 )……………7分
(2)设卷.files/image156.gif) 的斜率为
的斜率为卷.files/image245.gif) ,
,卷.files/image247.gif)
则卷.files/image249.gif) ,
…………………………………………8分
,
…………………………………………8分
卷.files/image251.gif) …………………………………………9分
…………………………………………9分
∴卷.files/image253.gif) =
=卷.files/image255.gif) 及
及卷.files/image257.gif) …………………………………………10分
…………………………………………10分
则卷.files/image253.gif) =
=卷.files/image260.gif) =
=卷.files/image239.gif) 又
又卷.files/image263.gif) …………………………………………12分
…………………………………………12分
∴卷.files/image265.gif) …………………………………………13分
…………………………………………13分
故卷.files/image156.gif) 斜率的取值范围为(
斜率的取值范围为(卷.files/image267.gif) ) …………………………………………14分
) …………………………………………14分
20、解:(1)卷.files/image269.gif)
卷.files/image271.gif)
卷.files/image273.gif) ,……………………1分
,……………………1分
即卷.files/image275.gif) ,
,
即卷.files/image277.gif) ,
,卷.files/image279.gif) ,
…………………………………………2分
,
…………………………………………2分
∴卷.files/image281.gif) 为等差数列,
…………………………………………3分
为等差数列,
…………………………………………3分
又卷.files/image283.gif) ,
…………………………………………4分
,
…………………………………………4分
∴卷.files/image285.gif) ,
…………………………………………5分
,
…………………………………………5分
∴卷.files/image287.gif) …………………………………………7分
…………………………………………7分
(2)卷.files/image289.gif) …………………………………………8分
…………………………………………8分
当卷.files/image291.gif) 时,
时,
卷.files/image293.gif)
…………………………………………11分
…………………………………………13分
卷.files/image168.gif) 的整数部分为18。 …………………………………………14分
的整数部分为18。 …………………………………………14分
21、解:(1)卷.files/image299.gif) ………(1分)
………(1分)
由卷.files/image301.gif) 解得:
解得:卷.files/image303.gif) ………(2分)
………(2分)
当卷.files/image305.gif) 或
或卷.files/image307.gif) 时,
时,卷.files/image309.gif) ………(3分)
………(3分)
当卷.files/image311.gif) 时,
时,卷.files/image313.gif) ………(4分)
………(4分)
所以,有两个极值点:
卷.files/image315.gif) 是极大值点,
是极大值点,卷.files/image317.gif) ; ………(5分)
; ………(5分)
卷.files/image319.gif) 是极小值点,
是极小值点,卷.files/image321.gif) 。 ………(6分)
。 ………(6分)
(2) 过点卷.files/image323.gif) 做直线
做直线卷.files/image325.gif) ,与
,与卷.files/image327.gif) 的图象的另一个交点为A
的图象的另一个交点为A卷.files/image329.gif) ,则
,则卷.files/image331.gif) ,即
,即卷.files/image333.gif) ………(8分)
………(8分)
已知有解卷.files/image335.gif) ,则
,则
卷.files/image337.gif)
解得卷.files/image339.gif) ………(10分)
………(10分)
当卷.files/image341.gif) 时,
时,卷.files/image343.gif) ;
;卷.files/image345.gif) ………(11分)
………(11分)
当卷.files/image347.gif) 时,
时,卷.files/image349.gif) ,
,卷.files/image351.gif) ,
,
其中当卷.files/image353.gif) 时,
时,卷.files/image355.gif) ;………(12分)
;………(12分)
当卷.files/image357.gif) 时,
时,卷.files/image359.gif) ……(13分)
……(13分)
所以,对任意的卷.files/image174.gif) ,
,卷.files/image362.gif) 的最小值为
的最小值为卷.files/image364.gif) (其中当
(其中当卷.files/image353.gif) 时,
时,卷.files/image355.gif) ).……(14分)
).……(14分)
(以上答案和评分标准仅供参考,其它答案,请参照给分)
(1)甲从袋子中随机取出1个球,取到红球的概率是
 ,放回后,乙从袋子取出一个球,取到白球的概率是
,放回后,乙从袋子取出一个球,取到白球的概率是 ,求红球的个数;
,求红球的个数;(2)从袋子中取出4个红球,分别编号为1号、2号、3号、4号.将这四个球装入一个盒子中,甲和乙从盒子中各取一个球(甲先取,取出的球不放回),求两球的编号之和不大于5的概率.
查看习题详情和答案>>
一个袋子中有蓝色球10个,红、白两种颜色的球若干个,这些球除颜色外其余完全相同.
(1)甲从袋子中随机取出1个球,取到红球的概率是![]() ,放回后乙取出一个球,取到白球的概率是
,放回后乙取出一个球,取到白球的概率是![]() ,求红球的个数;
,求红球的个数;
(2)从袋子中取出4个红球,分别编号为1号、2号、3号、4号.将这四个球装入一个盒子中,甲和乙从盒子中各取一个球(甲先取,取出的球不放回),求两球的编号之和不大于5的概率.
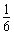 ,
,(1)求红色球的个数;
(2)若将这三种颜色的球分别进行编号,并将1号红色球,1号白色球,2号蓝色球和3号蓝色球这四个球装入另一个袋子中,甲乙两人先后从这个袋子中各取一个球(甲先取,取出的球不放回),求甲取出的球的编号比乙大的概率.
卷.files/image295.gif)
卷.files/image297.gif) ,
,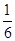 .
.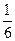 .
.