题目内容
一个袋子中有蓝色球10个,红、白两种颜色的球若干个,这些球除颜色外其余完全相同.(1)甲从袋子中随机取出1个球,取到红球的概率是
 ,放回后,乙从袋子取出一个球,取到白球的概率是
,放回后,乙从袋子取出一个球,取到白球的概率是 ,求红球的个数;
,求红球的个数;(2)从袋子中取出4个红球,分别编号为1号、2号、3号、4号.将这四个球装入一个盒子中,甲和乙从盒子中各取一个球(甲先取,取出的球不放回),求两球的编号之和不大于5的概率.
【答案】分析:(1)设红球有x个,白球y个,依题意中的概率得方程,从而求得红球的个数‘
(2)利用列举法写出甲和乙从盒子中各取一个球的方法总数,再从中观察得到两球的编号之和不大于5的种数,它们的比值即为所求概率.
解答:解:(1)设红球有x个,白球y个,依题意得(1分)
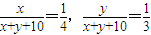 ,(3分)
,(3分)
解x=6故红球有6个.(6分)
(2)记“甲取出的球的编号大”为事件A,
所有的基本事件有:(1,2),(l,3),(1,4),
(2,1),(2,3),(2,4),
(3,1),(3,2),(3,4),
(4,1),(4,2),(4,3),
共12个基本事件(8分)
事件A包含的基本事件有:(1,2),(1,3),(1,4)(2,1),
(2,3),(3,1),(3,2)(4,1),
共8个基本事件(11分)
所以,.P(A)= (12分)
(12分)
点评:本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=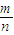 .
.
(2)利用列举法写出甲和乙从盒子中各取一个球的方法总数,再从中观察得到两球的编号之和不大于5的种数,它们的比值即为所求概率.
解答:解:(1)设红球有x个,白球y个,依题意得(1分)
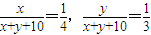 ,(3分)
,(3分)解x=6故红球有6个.(6分)
(2)记“甲取出的球的编号大”为事件A,
所有的基本事件有:(1,2),(l,3),(1,4),
(2,1),(2,3),(2,4),
(3,1),(3,2),(3,4),
(4,1),(4,2),(4,3),
共12个基本事件(8分)
事件A包含的基本事件有:(1,2),(1,3),(1,4)(2,1),
(2,3),(3,1),(3,2)(4,1),
共8个基本事件(11分)
所以,.P(A)=
 (12分)
(12分)点评:本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
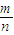 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目