摘要:所以数列为等比数列. ----------------4分
网址:http://m.1010jiajiao.com/timu_id_151910[举报]
下列五个命题:
①对于回归直线方程 ,
, 时,
时, .
.
②频率分布直方图中各小长方形的面积等于相应各组的频数.
③若 单调递增,则
单调递增,则 .
.
④样本 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 的平均值为
的平均值为 ,方差为
,方差为 .
.
⑤甲、乙两个乒乓球运动员进行乒乓球比赛,已知每一局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以用三局二胜或五局三胜制,相对于用五局三胜制,三局二胜制乙获胜的可能性更大.
其中正确结论的是 (填上你认为正确的所有序号).
查看习题详情和答案>>
下列五个命题:
①对于回归直线方程 ,
, 时,
时, .
.
②频率分布直方图中各小长方形的面积等于相应各组的频数.
③若 单调递增,则
单调递增,则 .
.
④样本 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 的平均值为
的平均值为 ,方差为
,方差为 .
.
⑤甲、乙两个乒乓球运动员进行乒乓球比赛,已知每一局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以用三局二胜或五局三胜制,相对于用五局三胜制,三局二胜制乙获胜的可能性更大.
其中正确结论的是 (填上你认为正确的所有序号).
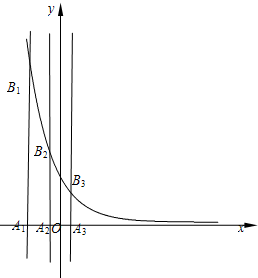 已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
查看习题详情和答案>>
已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数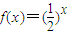 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
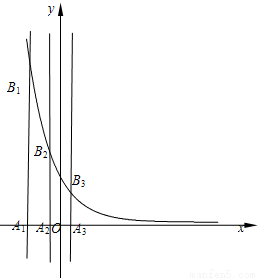
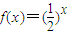 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 ,
,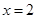 时,
时,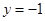 .
.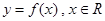 单调递增,则
单调递增,则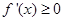 .
.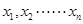 的平均值为
的平均值为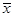 ,方差为
,方差为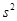 ,则
,则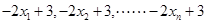 的平均值为
的平均值为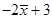 ,方差为
,方差为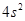 .
.