摘要：(Ⅲ)x的取值为0.1.2.3．
网址：http://m.1010jiajiao.com/timu_id_151836[举报]
（1）是否存在实数a．使f（x）=loga(ax-
)在区间[2，4]上是增函数．若存在求出a
（2）已知函数f（x）=lg（ax-kbx）（k∈R+a＞1＞b＞0）的定义域恰为区间（0，+∞），是否存在这样的a、b使得f（x）恰在（1，+∞）上取正值．且f（3）=lg4．若存在．求出a、b值．若不存在，说明理由． 查看习题详情和答案>>
| x |
（2）已知函数f（x）=lg（ax-kbx）（k∈R+a＞1＞b＞0）的定义域恰为区间（0，+∞），是否存在这样的a、b使得f（x）恰在（1，+∞）上取正值．且f（3）=lg4．若存在．求出a、b值．若不存在，说明理由． 查看习题详情和答案>>
（2012•北京）近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱，为调查居民生活垃圾分类投放情况，先随机抽取了该市三类垃圾箱总计1000吨生活垃圾，数据统计如下（单位：吨）；
（1）试估计厨余垃圾投放正确的概率；
（2）试估计生活垃圾投放错误的概率；
（3）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a，b，c，其中a＞0，a+b+c=600．当数据a，b，c的方差s2最大时，写出a，b，c的值（结论不要求证明），并求此时s2的值．
（求：S2=
[(x1-
) 2+(x2-
) 2+…+(xn-
) 2]，其中
为数据x1，x2，…，xn的平均数）
查看习题详情和答案>>
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
（2）试估计生活垃圾投放错误的概率；
（3）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a，b，c，其中a＞0，a+b+c=600．当数据a，b，c的方差s2最大时，写出a，b，c的值（结论不要求证明），并求此时s2的值．
（求：S2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
（1）是否存在实数a．使f（x）=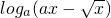
在区间[2，4]上是增函数．若存在求出a
（2）已知函数f（x）=lg（ax-kbx）（k∈R+a＞1＞b＞0）的定义域恰为区间（0，+∞），是否存在这样的a、b使得f（x）恰在（1，+∞）上取正值．且f（3）=lg4．若存在．求出a、b值．若不存在，说明理由．
查看习题详情和答案>>
（本小题满分13分）
某产品按行业生产标准分成8个等级，等级系数X依次为1,2，……，8，其中X≥5为标准A，X≥为标准B，已知甲厂执行标准A生产该产品，产品的零售价为6元/件；乙厂执行标准B生产该产品，产品的零售价为4元/件，假定甲、乙两厂得产品都符合相应的执行标准
（I）已知甲厂产品的等级系数X1的概率分布列如下所示：
|
| 5 | 6 | 7 | 8 |
| P | 0．4 | a | b | 0．1 |
且X1的数字期望EX1=6，求a，b的值；
（II）为分析乙厂产品的等级系数X2，从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X2的数学期望．
（III）在（I）、（II）的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可购买性？说明理由．
注：（1）产品的“性价比”=
；
（2）“性价比”大的产品更具可购买性．
查看习题详情和答案>>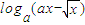
在区间[2，4]上是增函数．若存在求出a