摘要:(2)假设当1<<则.又在上单调递减.<<==.这说明时.命题也成立.
网址:http://m.1010jiajiao.com/timu_id_148995[举报]
对于不等式
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:
(1)当n=1时,
<1+1,不等式成立.
(2)假设当n=k(k∈N*)时,不等式成立,即
<k+1,则当n=k+1时,
=
<
=
=(k+1)+1,∴当n=k+1时,不等式成立.
则上述证法( )
| n2+n |
(1)当n=1时,
| 12+1 |
(2)假设当n=k(k∈N*)时,不等式成立,即
| k2+k |
| (k+1)2+(k+1) |
| k2+3k+2 |
| (k2+3k+2)+(k+2) |
| (k+2)2 |
则上述证法( )
| A、过程全部正确 |
| B、n=1验得不正确 |
| C、归纳假设不正确 |
| D、从n=k到n=k+1的推理不正确 |
对于不等式 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:
(1)当n=1时, <1+1,不等式成立.
<1+1,不等式成立.
(2)假设当n=k(k∈N*)时,不等式成立,即 <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
=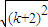 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.
则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:(1)当n=1时,
 <1+1,不等式成立.
<1+1,不等式成立.(2)假设当n=k(k∈N*)时,不等式成立,即
 <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
=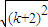 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>
对于不等式 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:
(1)当n=1时, <1+1,不等式成立.
<1+1,不等式成立.
(2)假设当n=k(k∈N*)时,不等式成立,即 <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.
则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:(1)当n=1时,
 <1+1,不等式成立.
<1+1,不等式成立.(2)假设当n=k(k∈N*)时,不等式成立,即
 <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>
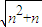 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立.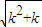 <k+1,则当n=k+1时,
<k+1,则当n=k+1时,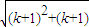 =
=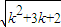 <
<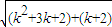 =
=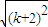 =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立. <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
<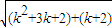 =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.