题目内容
对于不等式
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:
(1)当n=1时,
<1+1,不等式成立.
(2)假设当n=k(k∈N*)时,不等式成立,即
<k+1,则当n=k+1时,
=
<
=
=(k+1)+1,∴当n=k+1时,不等式成立.
则上述证法( )
| n2+n |
(1)当n=1时,
| 12+1 |
(2)假设当n=k(k∈N*)时,不等式成立,即
| k2+k |
| (k+1)2+(k+1) |
| k2+3k+2 |
| (k2+3k+2)+(k+2) |
| (k+2)2 |
则上述证法( )
| A、过程全部正确 |
| B、n=1验得不正确 |
| C、归纳假设不正确 |
| D、从n=k到n=k+1的推理不正确 |
分析:此证明中,从推出P(k+1)成立中,并没有用到假设P(k)成立的形式,不是数学归纳法.
解答:解:在n=k+1时,没有应用n=k时的假设,
即从n=k到n=k+1的推理不正确.
故选D.
即从n=k到n=k+1的推理不正确.
故选D.
点评:本题主要考查数学归纳法,数学归纳法的基本形式
设P(n)是关于自然数n的命题,若
1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立
设P(n)是关于自然数n的命题,若
1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
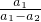
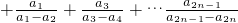 ,Qn=
,Qn=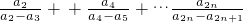 ,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.
,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.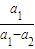
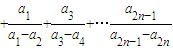 ,Qn=
,Qn=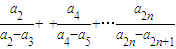 ,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.
,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.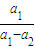
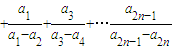 ,Qn=
,Qn=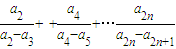 ,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.
,若r>c>4,求证:对于一切n∈N*,不等式-n<Pn-Qn<n2+n恒成立.