摘要:解析:.由函数图象的走向可知.单调性是先增后减再增.因此导函数的值应该是随由小到大.先正后负再为正.因此.从函数图象可以确定函数有两个极值点.易知方程有相异的两个实数根且负根的绝对值大.由根与系数的关系可判定.故选B.说明:本题难度较大.综合性强.如何从图中得出极点及单调性的特点是解决本题的关键.同时又要运用二次函数的性质解题.对一元二次方程根与系数的关系也进行了考查.由单调性开口方向,由极值点得方程的根,由方程的根再判定字母的取值,从中也体现出对学生的思维品质有较高的要求
网址:http://m.1010jiajiao.com/timu_id_148777[举报]
已知函数f(x)=
sin(2ωx-
)+b,且该函数图象的对称中心和对称轴的最小距离为
,当x∈[0,
]时,f(x)的最大值为
.
(1)求f(x)的解析式.
(2)画出f(x)在长度为一个周期内的简图(直接画图,不用列表).
(3)分步说明该函数的图象是由正弦曲线经过怎样的变化得到的.
查看习题详情和答案>>
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| 5 |
| 2 |
(1)求f(x)的解析式.
(2)画出f(x)在长度为一个周期内的简图(直接画图,不用列表).
(3)分步说明该函数的图象是由正弦曲线经过怎样的变化得到的.
已知函数y=2sin(ωx+φ)的最小正周是
,直线x=
是该函数图象的一条对称轴,则函数的解析式可以是( )
| π |
| 2 |
| π |
| 6 |
A、y=2sin(4x+
| ||
B、y=2sin(4x-
| ||
C、y=2sin(2x+
| ||
D、y=2sin(2x-
|
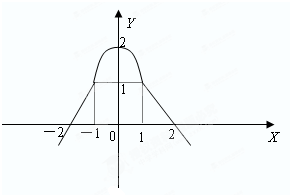 已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示
已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示 的值.
的值.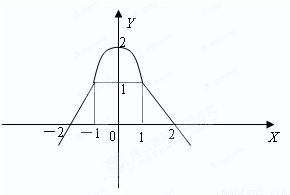
 已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示
已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示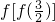 的值.
的值.