题目内容
已知y=f（x）的定义域为R，其图象是由两条射线和二次函数图象的一部分构成，其中（0，2）顶点，如图所示
（Ⅰ）求y=f（x）的解析式；
（Ⅱ）求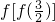
的值．
解：（I）当x≤-1时，设f（x）=kx+b
则由图象可知，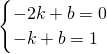
，解可得
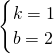
∴f（x）=x+2（x≤-1）
当x≥1时，设f（x）=mx+n
由图象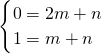可得，
，解可得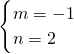
∴f（x）=-x+2
当-1＜x＜1，设f（x）=ax2+2
∵f（1）=a+2=1
∴a=1
∴
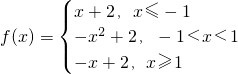
（2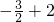）∵f（
）=
=
∴f[f（）]=f（）=
=
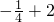分析：（I）结合图象可知，当x≤-1，x≥1时，函数为一次函数，设出函数的解析式，由函数图象所经过的点的坐标求解即可；当-1＜x＜1，函数为开口向下，对称轴为y轴的二次函数且f（1）=1可求函数解析式
（2）根据（I）可先求f（），然后进一步代入即可求解
点评：本题主要考查了利用待定系数法求解函数的解析式，解题的关键是由已知 函数图象找出函数所经过的已知点的坐标
则由图象可知，
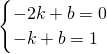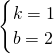
，解可得∴f（x）=x+2（x≤-1）
当x≥1时，设f（x）=mx+n
由图象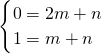可得，
，解可得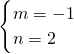∴f（x）=-x+2
当-1＜x＜1，设f（x）=ax2+2
∵f（1）=a+2=1
∴a=1
∴
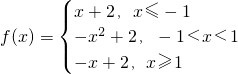
（2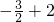）∵f（
）==∴f[f（
）]=f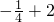（）==分析：（I）结合图象可知，当x≤-1，x≥1时，函数为一次函数，设出函数的解析式，由函数图象所经过的点的坐标求解即可；当-1＜x＜1，函数为开口向下，对称轴为y轴的二次函数且f（1）=1可求函数解析式
（2）根据（I）可先求f（
），然后进一步代入即可求解点评：本题主要考查了利用待定系数法求解函数的解析式，解题的关键是由已知 函数图象找出函数所经过的已知点的坐标
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，已知：射线OA为y=kx（k＞0，x＞0），射线OB为y=-kx（x＞0），动点P（x，y）在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k．
已知函数f（x）=x+
已知幂函数y=f（x）的图象经过点（2，4），对于偶函数y=g（x）（x∈R），当x≥0时，g（x）=f（x）-2x．
已知函数f（x）=2x+