网址:http://m.1010jiajiao.com/timu_id_14813[举报]
一.选择题:
题号
1
2
3
4
5
6
7
8
答案
C
A
C
B
B
A
B
D
二.填空题:
9.6、30、10;
10..files/image196.gif) ;
11.
;
11..files/image198.gif) ;
;
12..files/image200.gif) ;
13.{
;
13.{.files/image202.gif) 0<
0<.files/image044.gif) ≤3};
14.③④
≤3};
14.③④
三、 解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
15.解: .files/image205.gif) ; ………5分
; ………5分
.files/image207.gif) 方程
方程.files/image209.gif) 有非正实数根
有非正实数根.files/image211.gif)
.files/image213.gif)
综上:.files/image215.gif) ……………………12分
……………………12分
16. 解:(Ⅰ)设取出的4件中有2件合格品或3件合格品分别为事件A、B,则
.files/image217.gif)
∵A、B为两个互斥事件 ∴P(A+B)=P(A)+P(B)=.files/image219.gif)
答: 取出2件合格品或3件合格品的概率为.files/image219.gif) …………6分
…………6分
(Ⅱ)取出4件都为合格品的事件为C,则P(C)=.files/image221.gif)
至少取出一件次品的事件为事件C的对立事件,其概率为.files/image223.gif)
答:至少取出一件次品的概率为.files/image225.gif) .…………13分
.…………13分
17.解:(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2+2ax+b
由f¢(.files/image227.gif) )=
)=.files/image229.gif) ,f¢(1)=3+
,f¢(1)=3+
a=.files/image231.gif) ,b=-2。。。。。。。。。4分
,b=-2。。。。。。。。。4分
f¢(x)=3.files/image083.gif) 2-
2-.files/image083.gif) -2=(3
-2=(3.files/image083.gif) +2)(
+2)(.files/image083.gif) -1),函数f(x)的单调区间如下表:
-1),函数f(x)的单调区间如下表:
.files/image083.gif)
(-¥,-.files/image234.gif) )
)
-.files/image234.gif)
(-.files/image234.gif) ,1)
,1)
1
(1,+¥)
f¢(x)
+
0
-
0
+
f(x)
极大值
¯
极小值
所以函数f(.files/image083.gif) )的递增区间是(-¥,-
)的递增区间是(-¥,-.files/image234.gif) )与(1,+¥)
)与(1,+¥)
递减区间是(-.files/image234.gif) ,1)。。。。。。。。。。。7分
,1)。。。。。。。。。。。7分
(2)f(x)=.files/image083.gif) 3-
3-.files/image236.gif)
.files/image083.gif) 2-2
2-2.files/image083.gif) +c,
+c,.files/image083.gif) Î
Î.files/image110.gif) ,由(1)当
,由(1)当.files/image083.gif) =-
=-.files/image234.gif) 时,f(x)=
时,f(x)=.files/image238.gif) +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(.files/image083.gif) Î
Î.files/image110.gif) )恒成立,只需c
)恒成立,只需c
解得c<-1或c>2 。。。。。。。。。。。。13分
.files/image122.gif) 18.(Ⅰ)证明:∵
18.(Ⅰ)证明:∵.files/image126.gif) 底面
底面.files/image128.gif) ,
,.files/image242.gif) 底面
底面.files/image128.gif) ,∴
,∴.files/image244.gif)
又∵.files/image246.gif) 且
且.files/image248.gif) 平面
平面.files/image145.gif) ,
, .files/image251.gif) 平面
平面.files/image145.gif) ,
, .files/image253.gif) ,
,
∴.files/image143.gif) 平面
平面.files/image145.gif) ;
;.files/image255.gif) 4分
4分
(Ⅱ)解:∵点.files/image139.gif) 分别是
分别是.files/image141.gif) 的中点,
的中点,
∴.files/image258.gif) ,由(Ⅰ)知
,由(Ⅰ)知.files/image143.gif) 平面
平面.files/image145.gif) ,∴
,∴.files/image260.gif) 平面
平面.files/image145.gif) ,
,
∴.files/image260.gif)
.files/image262.gif) ,
,.files/image260.gif)
.files/image264.gif) ,
,
∴.files/image266.gif) 为二面角
为二面角.files/image147.gif) 的平面角,
的平面角,.files/image255.gif) 7分
7分
∵.files/image126.gif) 底面
底面.files/image128.gif) ,
,
∴.files/image134.gif) 与底面
与底面.files/image128.gif) 所成的角即为
所成的角即为.files/image268.gif) ,
,
∴.files/image268.gif) =
=.files/image137.gif) ,
,
∵.files/image271.gif) 为直角三角形
为直角三角形.files/image145.gif) 斜边
斜边.files/image134.gif) 的中点,
的中点,
∴.files/image275.gif) 为等腰三角形,且
为等腰三角形,且.files/image277.gif) ,
,
.files/image281.gif) ∴
∴.files/image266.gif)
.files/image284.gif) ,∴二面角
,∴二面角.files/image147.gif) 的大小为
的大小为.files/image286.gif) ;
;.files/image255.gif) 9分
9分
(Ⅲ)法1:过点.files/image288.gif) 作
作.files/image290.gif) 交
交.files/image292.gif) 于点
于点.files/image294.gif) ,则
,则.files/image296.gif) 或其补角即为异面直
或其补角即为异面直
线.files/image151.gif) 所成的角,
所成的角,.files/image255.gif) 11分
11分
∵.files/image288.gif) 为
为.files/image299.gif) 的中点,∴
的中点,∴.files/image294.gif) 为为
为为.files/image292.gif) 的中点, 设
的中点, 设.files/image303.gif) ,则由
,则由.files/image305.gif)
.files/image132.gif) 得
得.files/image307.gif) ,又
,又.files/image149.gif) ,∴
,∴.files/image309.gif) ∴
∴.files/image311.gif) =
=.files/image313.gif) ,∴
,∴.files/image315.gif) ,
,
∴由(Ⅱ)知.files/image317.gif) 为直角三角形,且
为直角三角形,且 .files/image319.gif) ,
,
.files/image321.gif) ,∴
,∴.files/image323.gif) ,
,
在直角三角形.files/image325.gif) 中,
中,.files/image327.gif) ,
,
∴.files/image329.gif) ,
,
∴在三角形.files/image331.gif) 中,
中,.files/image333.gif) ,
,.files/image255.gif) 13分
13分
∴.files/image335.gif) 为直角三角形,
为直角三角形,.files/image296.gif) 为直角,
为直角,
.files/image340.gif) ∴异面直线
∴异面直线.files/image151.gif) 所成的角为
所成的角为.files/image342.gif) .
..files/image255.gif) 14分
14分
或者用三垂线定理,首先证明DB与BC垂直也可以
因为.files/image309.gif) ∴
∴.files/image311.gif) =
=.files/image313.gif) ,又
,又.files/image344.gif) ,
,
所以.files/image346.gif) ,即DB与BC垂直
,即DB与BC垂直
法2:以点.files/image348.gif) 为坐标原点,建立如图的直角坐标系,设
为坐标原点,建立如图的直角坐标系,设.files/image350.gif) ,则
,则.files/image352.gif) ,
,.files/image354.gif) ,
,.files/image356.gif) ,则
,则
.files/image358.gif) 则
则.files/image360.gif) ,
,.files/image362.gif) ,
,.files/image364.gif) ,
,
.files/image366.gif)
.files/image368.gif)
.files/image370.gif) ,∴异面直线
,∴异面直线.files/image151.gif) 所成的角为
所成的角为.files/image342.gif) …………….
14分
…………….
14分
19.解:1)由.files/image081.gif) =
=.files/image372.gif) .
..files/image374.gif) =
=.files/image376.gif) ,∴
,∴.files/image159.gif) =1;……….4分
=1;……….4分
(2).files/image081.gif) =
=.files/image378.gif) 在(1,+∞)上是单调递减函数,
在(1,+∞)上是单调递减函数,
任取.files/image380.gif) 、
、.files/image382.gif) ∈(1,+∞),且设
∈(1,+∞),且设.files/image380.gif) <
<.files/image382.gif) ,则:
,则:
.files/image386.gif) -
-.files/image388.gif) =
=.files/image390.gif) >0,
>0,
∴.files/image081.gif) =
=.files/image378.gif) 在(1,+∞)上是单调递减函数;……………9分
在(1,+∞)上是单调递减函数;……………9分
(3)当直线.files/image157.gif) =
=.files/image044.gif) (
(.files/image044.gif) ∈R)与
∈R)与.files/image081.gif) 的图象无公共点时,
的图象无公共点时,.files/image044.gif) =1,
=1,
∴.files/image165.gif) <2+
<2+.files/image392.gif) =4=
=4=.files/image394.gif) ,|
,|.files/image169.gif) -2|+
-2|+.files/image396.gif) >2,
>2,
得:.files/image169.gif) >
>.files/image398.gif) 或
或.files/image169.gif) <
<.files/image396.gif) …………..14分
…………..14分
20.解.files/image400.gif)
(1)当.files/image180.gif) 时,
时, .files/image402.gif)
设.files/image083.gif) 为其不动点,即
为其不动点,即.files/image405.gif)
则.files/image407.gif)
.files/image409.gif) 的不动点是-1,2………..
4分
的不动点是-1,2………..
4分
(2)由.files/image411.gif) 得:
得:.files/image413.gif) . 由已知,此方程有相异二实根,
. 由已知,此方程有相异二实根,
.files/image415.gif) 恒成立,即
恒成立,即.files/image417.gif) 即
即.files/image419.gif) 对任意
对任意.files/image421.gif) 恒成立.
恒成立.
.files/image423.gif) …………………. …………10分
…………………. …………10分
(3)设.files/image425.gif) ,
,
直线.files/image427.gif) 是线段AB的垂直平分线, ∴
是线段AB的垂直平分线, ∴ .files/image429.gif)
记AB的中点.files/image431.gif) 由(2)知
由(2)知.files/image433.gif)
.files/image435.gif)
化简得:.files/image437.gif) 时,等号成立).
时,等号成立).
.files/image439.gif) ……………………………………………………………14分
……………………………………………………………14分




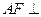 平面
平面 ;
;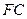 的中点为
的中点为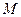 ,求证:
,求证: 平面
平面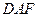 ;
; 的体积.
的体积.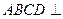 平面
平面 ;
;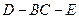 的平面角的正切值.
的平面角的正切值.