摘要:的结论有
网址:http://m.1010jiajiao.com/timu_id_14769[举报]
(2011•上海)对于给定首项x0>
(a>0),由递推公式xn+1=
(xn+
)(n∈N)得到数列{xn},对于任意的n∈N,都有xn>
,用数列{xn}可以计算
的近似值.
(1)取x0=5,a=100,计算x1,x2,x3的值(精确到0.01);归纳出xn,xn+1,的大小关系;
(2)当n≥1时,证明:xn-xn+1<
(xn-1-xn);
(3)当x0∈[5,10]时,用数列{xn}计算
的近似值,要求|xn-xn+1|<10-4,请你估计n,并说明理由.
查看习题详情和答案>>
| 3 | a |
| 1 |
| 2 |
|
| 3 | a |
| 3 | a |
(1)取x0=5,a=100,计算x1,x2,x3的值(精确到0.01);归纳出xn,xn+1,的大小关系;
(2)当n≥1时,证明:xn-xn+1<
| 1 |
| 2 |
(3)当x0∈[5,10]时,用数列{xn}计算
| 3 | 100 |
在数列{an}中,a1=a,以后各项由递推公式an+1=
给出,写出这个数列的前4项:
、
、
,并由此写出一个通项公式an=
.
查看习题详情和答案>>
| 2an |
| 1+an |
a
a
、| 2a |
| 1+a |
| 2a |
| 1+a |
| 4a |
| 1+3a |
| 4a |
| 1+3a |
| 8a |
| 1+7a |
| 8a |
| 1+7a |
| 2n-1a |
| 1+(2n-1-1)a |
| 2n-1a |
| 1+(2n-1-1)a |
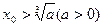 ,由递推公式
,由递推公式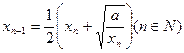 得到数列
得到数列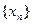 ,对于任意的
,对于任意的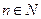 ,都有
,都有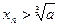 ,用数列
,用数列 的近似值。
的近似值。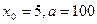 ,计算
,计算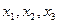 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出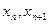 的大小关系;
的大小关系;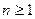 时,证明:
时,证明: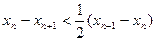 ;
;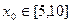 时,用数列
时,用数列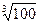 的近似值,要求
的近似值,要求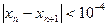 ,请你估计n,并说明理由
,请你估计n,并说明理由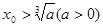 ,由递推公式
,由递推公式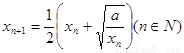 得到数列
得到数列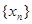 ,对于任意的
,对于任意的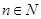 ,都有
,都有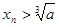 ,用数列
,用数列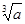 的近似值。
的近似值。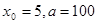 ,计算
,计算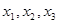 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出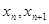 的大小关系;
的大小关系;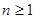 时,证明:
时,证明: ;
;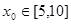 时,用数列
时,用数列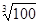 的近似值,要求
的近似值,要求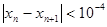 ,请你估计n,并说明理由
,请你估计n,并说明理由