网址:http://m.1010jiajiao.com/timu_id_135715[举报]
(本大题满分14分)
2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数(以百人为计数单位)作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计数人数的时间,即![]() ;9点20分作为第二个计数人数的时间,即
;9点20分作为第二个计数人数的时间,即![]() ;依此类推
;依此类推![]() ,把一天内从上午9点到晚上24点分成了90个计数单位.第
,把一天内从上午9点到晚上24点分成了90个计数单位.第![]() 个时刻进入园区的人数
个时刻进入园区的人数![]() 和时间
和时间![]() (
(![]() )满足以下关系:
)满足以下关系:  ,
,![]()
第![]() 个时刻离开园区的人数
个时刻离开园区的人数![]() 和时间
和时间![]() 满足以下关系:
满足以下关系:  .
.
(1)试计算在当天下午3点整(即15点整)时,世博园区内共有游客多少百人?(提示:![]() ,结果仅保留整数)
,结果仅保留整数)
(2)问:当天什么时刻世博园区内游客总人数最多?
查看习题详情和答案>>已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式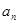 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当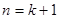 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
查看习题详情和答案>>
(本小题满分12分)
某校有一贫困学生因病需手术治疗,但现在还差手术费1.1万元.团委计划在全校开展爱心募捐活动,为了增加活动的趣味性吸引更多学生参与,特举办“摇奖100%中奖”活动.凡捐款10元便可享受一次摇奖机会,如图是摇奖机的示意图,摇奖机的旋转盘是均匀的,扇形区域A,B,C,D,E所对应的圆心角的比值分别为1:2:3:4:5.相应区域分别设立一、二、三、四、五等奖,奖品分别为价值5元、4元、3元、2元、1元的学习用品.摇奖时,转动圆盘片刻,待停止后,固定指针指向哪个区域(边线忽略不计)即可获得相应价值的学习用品(如图指针指向区域,可获得价值3元的学习用品).
(1)预计全校捐款10元者将会达到1500人次,那么除去购买学习用品的款项后,剩余款项是否能帮助该生完成手术治疗?
(2)如果学生甲捐款20元,获得了两次摇奖机会,求他获得价值6元时的学习用品的概率.

(本小题满分12分)已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼.为了估计池塘中这两种鱼的数量,养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只,给每只鱼作上不影响其存活的记号,然后放回池塘,经过一定时间,再每次从池塘中随机地捕出1000只鱼,分类记录下其中有记号的鱼的数目,随即将它们放回池塘中.这样的记录作了10次,将记录获取的数据作成如右的茎叶图.
(Ⅰ)根据茎叶图计算有记号的红鲫鱼与中国金鱼数目的平均数,并估计池塘中的红鲫鱼与中国金鱼的数量;
(Ⅱ)随机从池塘中逐只、有放回地捕出3只鱼,求恰好是1只中国金鱼、2只红鲫鱼的概率.

(本小题满分12分)某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在![]() 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.


表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率
分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 |
|
| |
| 不合格品 |
|
| |
| 合 计 |
|
附:下面的临界值表供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()