摘要:(3)性质1的另一种解释:从n个不同的元素中取出m个元素.并成一组.那么.剩下的n-m个元素也成一组,反之.从n个不同的元素中取出n-m个元素并组成一组.那么剩下的m个元素也成一组.所以.它们的组合是一一对应的.故有从n个不同的元素中取出m个的组合数是等于从 n个不同的元素中取出n-m个元素的组合数.即=.
网址:http://m.1010jiajiao.com/timu_id_13473[举报]
阅读下列材料,按要求回答问题.
(1)观察下面两块三角尺,它们有一个共同的性质:∠A=2∠B,我们由此出发来进行思考.
在图(1)中作斜边上的高CD,由于∠B=30°,可知c=2b,∠ACD=30°,于是AD=
,BD=c-
,由于△CDB∽△ACB,可知,即a2=c•BD.同理b2=c•AD,于是a2-b2=c(BD-AD)=c(c-b)=bc.对于图(2),由勾股定理有a2=b2+c2,由于b=c,故也有a2-b2=bc.
在△ABC中,如果一个内角等于另一个内角的2倍,我们称这样的三角形为倍角三角形,两块三角尺都是特殊的倍角三角形,对于任意倍角三角形,上面的结论仍然成立吗?我们暂时把设想作为一种猜测:
如图(3),在△ABC中,若∠CAB=2∠ABC,则a2-b2=bc.
在上述由三角尺的性质到“猜测”这一认识过程中,用到了下列四种数学思想方法中的哪一种选出一个正确的并将其序号填在括号内( )
①分类的思想方法②转化的思想方法③由特殊到一般的思想方法④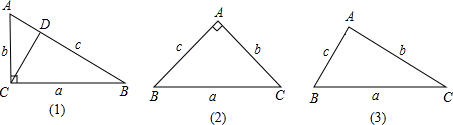 数形结合的思想方法
数形结合的思想方法
(2)这个猜测是否正确,请证明. 查看习题详情和答案>>
(1)观察下面两块三角尺,它们有一个共同的性质:∠A=2∠B,我们由此出发来进行思考.
在图(1)中作斜边上的高CD,由于∠B=30°,可知c=2b,∠ACD=30°,于是AD=
| b |
| 2 |
| b |
| 2 |
在△ABC中,如果一个内角等于另一个内角的2倍,我们称这样的三角形为倍角三角形,两块三角尺都是特殊的倍角三角形,对于任意倍角三角形,上面的结论仍然成立吗?我们暂时把设想作为一种猜测:
如图(3),在△ABC中,若∠CAB=2∠ABC,则a2-b2=bc.
在上述由三角尺的性质到“猜测”这一认识过程中,用到了下列四种数学思想方法中的哪一种选出一个正确的并将其序号填在括号内( )
①分类的思想方法②转化的思想方法③由特殊到一般的思想方法④
 数形结合的思想方法
数形结合的思想方法(2)这个猜测是否正确,请证明. 查看习题详情和答案>>
金属在日常生活中随处可见,研究金属的性质可以更好地利用金属。
(1)铝、铁、铜是常见金属。下列生活用品中,主要利用金属导热性的是 (填序号)。

(2)“淬火”是金属热处理常用的方法。宝剑淬火过程中,铁在高温下和水蒸气发生反应生成四氧化三铁和另一种气体单质,此反应的化学方程式为 ,该反应属于基本反应类型中的 反应。
(3)将一定量铁粉加入到硫酸锌、硫酸铜的混合液中,充分反应后过滤。滤液中的溶质一定有 。
(4)取一定量镁、锌、铁三种金属,分别加入溶质质量分数相等的稀盐酸,充分反应后,生成氢气的质量相等。下列做法能达到上述结果的是 (填序号)。
查看习题详情和答案>>
(1)铝、铁、铜是常见金属。下列生活用品中,主要利用金属导热性的是 (填序号)。

(2)“淬火”是金属热处理常用的方法。宝剑淬火过程中,铁在高温下和水蒸气发生反应生成四氧化三铁和另一种气体单质,此反应的化学方程式为 ,该反应属于基本反应类型中的 反应。
(3)将一定量铁粉加入到硫酸锌、硫酸铜的混合液中,充分反应后过滤。滤液中的溶质一定有 。
(4)取一定量镁、锌、铁三种金属,分别加入溶质质量分数相等的稀盐酸,充分反应后,生成氢气的质量相等。下列做法能达到上述结果的是 (填序号)。
| A.相同质量的三种金属与足量的稀盐酸反应 |
| B.2.4 g镁、6.5 g锌、5.6 g铁与足量的稀盐酸反应 |
| C.向足量的镁、锌、铁中加入稀盐酸的质量比为2︰2︰3 |
| D.足量的三种金属与等量的稀盐酸反应 |
如图,在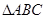 中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
求证:DE = DF.

证明: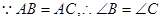 (①
)
(①
)
在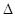 BDE和
BDE和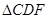 中,
中,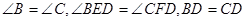 ,
,
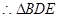 ≌
≌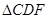 (②
)
(②
)
 (③
)
(③
)
⑴上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.
⑵请你写出另一种证明此题的方法.
【解析】(1)D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
(2)连接AD,利用角平分线的性质求证
查看习题详情和答案>>
阅读下列材料,按要求回答问题.
(1)观察下面两块三角尺,它们有一个共同的性质:∠A=2∠B,我们由此出发来进行思考.
在图(1)中作斜边上的高CD,由于∠B=30°,可知c=2b,∠ACD=30°,于是AD= ,BD=c-
,BD=c- ,由于△CDB∽△ACB,可知,即a2=c•BD.同理b2=c•AD,于是a2-b2=c(BD-AD)=c(c-b)=bc.对于图(2),由勾股定理有a2=b2+c2,由于b=c,故也有a2-b2=bc.
,由于△CDB∽△ACB,可知,即a2=c•BD.同理b2=c•AD,于是a2-b2=c(BD-AD)=c(c-b)=bc.对于图(2),由勾股定理有a2=b2+c2,由于b=c,故也有a2-b2=bc.
在△ABC中,如果一个内角等于另一个内角的2倍,我们称这样的三角形为倍角三角形,两块三角尺都是特殊的倍角三角形,对于任意倍角三角形,上面的结论仍然成立吗?我们暂时把设想作为一种猜测:
如图(3),在△ABC中,若∠CAB=2∠ABC,则a2-b2=bc.
在上述由三角尺的性质到“猜测”这一认识过程中,用到了下列四种数学思想方法中的哪一种选出一个正确的并将其序号填在括号内
①分类的思想方法②转化的思想方法③由特殊到一般的思想方法④ 数形结合的思想方法
数形结合的思想方法
(2)这个猜测是否正确,请证明.
查看习题详情和答案>>
某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去.例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方….请你协助他们探索这个问题.
(1)写出判定扇形相似的一种方法:若 ,则两个扇形相似;
(2)有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧长为 ;
(3)如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心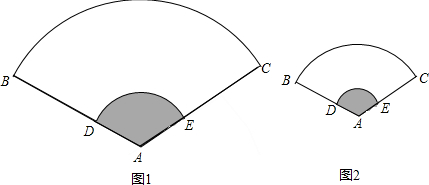 角和半径.
查看习题详情和答案>>
角和半径.
查看习题详情和答案>>
(1)写出判定扇形相似的一种方法:若
(2)有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧长为
(3)如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心
 角和半径.
查看习题详情和答案>>
角和半径.
查看习题详情和答案>>