题目内容
如图,在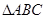 中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
求证:DE = DF.

证明: (①
)
(①
)
在 BDE和
BDE和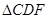 中,
中,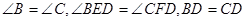 ,
,
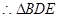 ≌
≌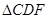 (②
)
(②
)
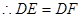 (③
)
(③
)
⑴上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.
⑵请你写出另一种证明此题的方法.
【解析】(1)D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
(2)连接AD,利用角平分线的性质求证
【答案】
解:(1)①等边对等角;
②AAS;
③全等三角形的对应边相等。
(2)证明连接AD

∵AB =AC,D是BC的中点,
∴AD平分∠BAC.
又DE⊥AB于E,DF⊥AC于F,
∴DE =DF.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目

 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 
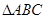 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 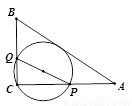
 中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.
中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.
 中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )