摘要:4.归纳结论: 两个相互独立事件同时发生的概率.等于每个事件发生的概率的积.我们把两个事件A.B同时发生记作A?B.则有P推广:如果事件A1.A2.-An相互独立.那么这n个事件同时发生的概率.等于每个事件发生的概率的积.即:P(A1?A2?-?An)= P(A1)?P(A2)?-?P(An)
网址:http://m.1010jiajiao.com/timu_id_13441[举报]
22、请先观察下列算式,再填空:
32-12=8×1
52-32=8×2
(1)72-52=8×
(2)92-(
(3)(
(4)132-(
通过观察归纳,写出反映这种规律的一般结论:
查看习题详情和答案>>
32-12=8×1
52-32=8×2
(1)72-52=8×
3
(2)92-(
7
)2=8×4(3)(
11
)2-92=8×5(4)132-(
11
)2=8×6
…通过观察归纳,写出反映这种规律的一般结论:
两个连续奇数的平方差能被8整除;或是8的倍数
.23、如图,在△ABC中,∠B=2∠C.现有两个条件:①AD为△ABC的高;②AD为△ABC的中线,请从中选择一个条件,并解答下面的问题:
(1)选择条件
(2)比较图中线段可以发现:AB+BD=

查看习题详情和答案>>
(1)选择条件
①
;(填所选条件的序号)(2)比较图中线段可以发现:AB+BD=
DC
(填图中的某一线段);证明你的结论.(下面两个图形供解题时选用)
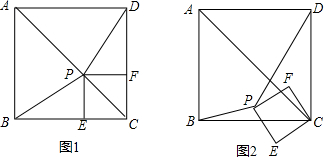
如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1)试说明:BP=DP;
(2)如图2,若正方形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请画图用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与正方形PECF的两个顶点连接,使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论;
(4)旋转的过程中AP和DF的长度是否相等,若不等,直接写出AP:DF= ;
(5)若正方形ABCD的边长是4,正方形PECF的边长是1.把正方形PECF绕点C按逆时针方向旋转的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)试说明:BP=DP;
(2)如图2,若正方形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请画图用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与正方形PECF的两个顶点连接,使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论;
(4)旋转的过程中AP和DF的长度是否相等,若不等,直接写出AP:DF=
(5)若正方形ABCD的边长是4,正方形PECF的边长是1.把正方形PECF绕点C按逆时针方向旋转的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
下列说法:
①方程x2-2x+3=0有两个正实数根;
②相等的圆心角所对的弧相等;
③均有一个角为100°的两个等腰三角形相似;
④若两个圆的圆心距小于两圆的半径之和,则两圆的位置关系可以是相交、内切、内含.
以上结论正确的个数是( )
①方程x2-2x+3=0有两个正实数根;
②相等的圆心角所对的弧相等;
③均有一个角为100°的两个等腰三角形相似;
④若两个圆的圆心距小于两圆的半径之和,则两圆的位置关系可以是相交、内切、内含.
以上结论正确的个数是( )
查看习题详情和答案>>
下列说法正确的是( )
| A、抛掷一枚正方体骰子,掷得的点数不会小于2是必然事件 | ||
B、在一个不透明的口袋中装有2个红球、2个黑球,这些球除颜色外其他都相同,在看不到球的条件下,随机地从这个袋子中一次摸出两个球,摸到两个球都是红球的概率是
| ||
| C、小华到文具店买文具时,营业员告诉他:买1支钢笔和2本练习本需4元钱,若买2支钢笔和1本练习本需5元钱.若小华只买1支钢笔和1本练习本,他付给营业员的钱为4元 | ||
| D、0.00020080有效数字的个数为9位 |