网址:http://m.1010jiajiao.com/timu_id_132096[举报]
二、13. 3 14.4 15. 16.
三、解答题
17.解:(I)∵(2a-c)cosB=bcosC,
∴(2sinA-sinC)cosB=sinBcosC. …………………2分
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA ………………………4分
∵0<A<π,∴sinA≠0.
∴cosB= …………………………………………5分
∵0<B<π,∴B= ………………………………………6分
(II)=4ksinA+cos2A. ……………………………………7分
=-2sin2A+4ksinA+1,A∈(0,)……………………………………9分
设sinA=t,则t∈.
则=-2t2+4kt+1=-2(t-k)2+1+2k2,t∈.…………………………10分
∵k>1,∴t=1时,取最大值.
依题意得,-2+4k+1=5,∴k=.………………………………………………12分
18. 解:设某一粒种子成功发芽为事件A,某一粒种子发生基因突变为事件B则其概率分别是
P(A)=,P(B)= ……………………2分
(1)这种“太空种子”中的某一粒种子既发芽又发生基因突变的概率
……………………7分
(2)四粒这种“太空种子”中至少有两粒既发芽又发生基因突变的概率是 …………………12分
19.解:(!)由已知可得
当时,两式相减得
即.当时,得
,从而,故总有,,
又从而,即数列是以6为首项,2为公比的等比数列.
则. ………6分
(2)由(1)知,, ………8分
从而则
………12分
则由题意得EF∥DA1,且EF=DA1,
∴四边形EFDA1是平行四边形
∴A1E∥FD,又A1E平面BDC1,FD平面BDC1
∴A1E∥平面BDC1 …6分
(2)由A1E⊥B1C1,A1E⊥CC1,得A1E⊥平面CBB1C1,过点E作
EH⊥BC1于H,连结A1H,则∠A1HE为二面角A1-BC1-B1的平面角 …8分
在Rt△BB1C1中,由BB1=8,B1C1=4,得BC1边上的高为,∴EH=,
又A1E=2,∴tan∠A1HE==>∴∠A1HE>60°, …11分
∴M在棱AA1上时,二面角M-BC1-B1总大于60°,故棱AA1上不存在使二面角M-BC1-B1的大小为60°的点M. …12分
D(2,40),A1(2,8,0), C1(0,8,2),B1(-2,8,0), E(-1,8,),
=(-4,-4,0), =(-2,4,2),=(-3,0, ),
=(-4,-8, 0), =(-2,0, 2),=(0,8,0),
=(2,8, 2).
(1)证明:∵=2(+)∴A1E∥平面BDC1 …6分
(2)设=(x,y,1)为平面A1BC1的一个法向量,则,且,即解得∴=(,,1),同理,设=(x,y,1)为平面B1BC1的一个法向量,则,且,即解得∴=(-,0,1),∴cos<,>==-
∴二面角A1-BC1-B1为arccos. 即arctan,又∵>
∴二面角A1-BC1-B1大于60°, ∴M在棱AA1上时,二面角M-BC1-B1总大于60°,故棱AA1上不存在使二面角M-BC1-B1的大小为60°的点M. ………… 12分
21解:(1)易知, ……………………………1分
所以,设,则
……4分
因为,故当时,即点P为椭圆短轴端点时,有最小值-2,
当时,即点P为椭圆长轴端点时,有最大值1. ……………………6分
(2)显然直线不满足题设条件; … …………………………7分
可设直线:,,
联立,消去整理得,
,
由得 ① ………9分
又,则又,
又
=,,
② ……………11分
故由①②得的取值范围是 .………………12分
22.(文)解:(1),由题意得,解得,经检验满足条…4分
(2)由(1)知,,………5分
令,则,(舍去).
的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
-
0
+
-1
ㄋ
-4
ㄊ
-3
∴在上单调递减,在上单调递增,
∴,如图构造在上的图象.
又关于x的方程在上恰有两个不同的实数根,
则,即m的取值范围是. ………8分
(3)解法一:因存在,使得不等式成立,
故只需要的最大值即可,
∵,∴.………………………10分
①若,则当时,,在单调递减.
,∴当时,,
∴当时,不存在,使得不等式成立.……………12分
②当a>0时随x的变化情况如下表:
x
+
0
-
ㄊ
ㄋ
∴当时,,由得.
综上得a>3,即a的取值范围是(3,+∞). … ………………………………14分
解法二:根据题意,只需要不等式在上有解即可,即在上有解. 即不等式在上有解即可. …………………………………10分
令,只需要 ………12分
而,当且仅当,即时“=”成立.
故a>3,即a的取值范围是(3,+∞). ………14分
(2)直线x+my+1=0与抛物线y2=2x交于点P,Q,在抛物线上是否存在点M,使得△MPQ为以PQ为斜边的直角三角形? 查看习题详情和答案>>
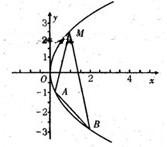 过抛物线C:y2=2px(p>0)上一点M(
过抛物线C:y2=2px(p>0)上一点M(| p | 2 |
(1)求证:直线AB的斜率为定值;
(2)已知A、B两点均在抛物线C:y2=2px(y≤0)上,若△MAB的面积的最大值为6,求抛物线的方程. 查看习题详情和答案>>
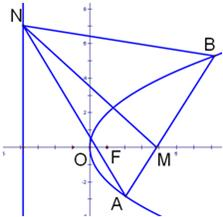 过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m>0),作直线AB与抛物线相交于A,B两点.
过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m>0),作直线AB与抛物线相交于A,B两点.(1)试证明A,B两点的纵坐标之积为定值;
(2)若点N是定直线l:x=-m上的任意一点,分别记直线AN,MN,BN的斜率为k1、k2、k3,
试求k1、k2、k3之间的关系,并给出证明. 查看习题详情和答案>>