网址：http://m.1010jiajiao.com/timu_id_13113[举报]
一、选择题：本大题共10小题，每小题5分，共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
D
A
C
B
A
C
B
C
二、填空题：本大题共4小题，每小题5分，共20分.其中12题的第一个空3分，第二
个空2分.
11.
.
12.
.
13.
.
14.
.
三、解答题：本大题共6小题，共80分.解答应写出文字说明、演算步骤或推证过程.
15．解：(1) 根据题意，可知
，
，即
. ……………………………2分
于是
. ………………………………………………………………………………………………3分
将点
代入
，得
即
. …………………………………………………………5分
满足的最小正数
. ……………………………………………………………7分
从而所求的函数解析式是
. ……………………………………………8分
(2)略.（振幅变换1分.周期变换、相位变换做对一个2分，全对3分） ……12分
16．解：显然
是随机变量.
(1)
.
. …………………………………6分
(2)由
的期望为
，得
，即
. …………………9分
根据表中数据，得
，即
. ………………………………………………11分
联立解得
. …………………………………………………………………………………………12分
17.解：(1)连结PQ，AQ.
∵△PCD为正三角形， ∴PQ⊥CD.
∵底面ABCD是∠ADC
的菱形，∴AQ⊥CD.
∴CD⊥平面PAQ. ………………………………………………………………………………………………4分
∴PA⊥CD.
(2)设平面CDM交PA于N，∵CD//AB， ∴CD//平面PAB. ∴CD//MN.
由于M为PB的中点，∴N为PA的中点. 又PD=CD=AD，∴DN⊥PA.
由(1)可知PA⊥CD， ∴PA⊥平面CDM. ………………………………8分
∴平面CDM⊥平面PAB.
∵PA⊥平面CDM，联接QN、QA，则ÐAQN为AQ与平面CDM所成的角. ……10分
在RtDPMA中，AM=PM=
，
∴AP=
，∴AN=
，sinÐAQN=
=
.
∴ÐAQN =45°.…………………………………………………14分
(2)另解（用空间向量解）：
由(1)可知PQ⊥CD，AQ⊥CD.
又由侧面PDC⊥底面ABCD，得PQ⊥AQ.
因此可以如图建立空间直角坐标系
. ………………………………………………………6分
易知P(0 , 0 ,)、A(, 0 , 0)、B(, 2 , 0)、
C（0 , 1 , 0）、D（0 , -1 , 0）. ………………………………………………………………………………7分
①由
=（, 0 , -），
=（0 , -2 , 0），得
×
=0.
∴PA⊥CD. ……………………………………………………………………………………………………………9分
②由M（
, 1 , -），
=（, 0 , -），得×
=0.
∴PA⊥CM . ……………………………………………………………………10分
∴PA⊥平面CDM，即平面CDM⊥平面PAB.
从而就是平面CDM的法向量.………………………12分
设AQ与平面所成的角为q ，
则sinq =|cos<
,>|=
.
∴AQ与平面所成的角为45°.……………………14分
18．解：(1)根据题意，
有解，
∴
即
. ……………………………………………………………………………3分
(2)若函数
可以在
和
时取得极值，
则有两个解和，且满足.
易得
. ………………………………………………………………………………………………6分
(3)由(2)，得
. ………………………………………………………………7分
根据题意，
(
)恒成立. ……………………………………………9分
∵函数
（）在时有极大值（用求导的方法），
且在端点
处的值为
.
∴函数（）的最大值为. …………………………13分
所以
. …………………………………………………………………………………………………………14分
19．解：(1)由于椭圆
过点
，故
.…………………………………1分
,
横坐标适合方程
解得
(
即
)．………………………………………………………4分
即,横坐标是(即).……………………………………5分
(2)根据题意，可设抛物线方程为
． …………………6分
∵
，∴
．………………………………………………………………7分
把
和（等同于,坐标（
，
））代入式抛物线方
程，得
. ……………………………………9分
令
．……………………………………10分
则
内有根（并且是单调递增函数），
∴
………………………………………………………………13分
解得
． …………………………………………………………………………………………14分
20．解：（1）∵f1(0)=2，a1=
=
，fn+1(0)= f1［fn(0)］=
, …………2分
∴an+1=
=
=
= -
= -an. ……………4分
∴数列｛an｝是首项为,公比为-的等比数列，∴an=(
)n-1. ………………5分
（2）∵T2 n = a1+
∴T2 n= (-a1)+(-)))(2n-1)a2 n－1+
2na2 n
= a 2+
两式相减，得
T2 n= a1+a2+a 3+…+a2 n+na2 n. ……………………………………………………7分
∴T2n =
+n×(-)2n-1=
-(-)2n+
(-)2n-1.
T2n =
-(-)2n+
(-)2n-1=(1-
). ……………9分∴9T2n=1-.
又Qn=1-
， ……………………………………………………………………………………………10分
当n=1时，22 n= 4,(2n+1)2=9,∴9T2 n＜Q n； ……………………………………………………11分
当n=2时，22 n=16,(2n+1)2=25,∴9T2 n＜Qn； …………………………………………………12分
当n≥3时，
，
∴9T2 n＞Q n. …………………………………………………………………………………………………………14分
①存在实数m，使得f（m）=0，且对任意实数x，恒有f（x）≥0成立；
②存在实数k （k≠0），使得f（1-k）=f（1+k）成立．
（1）求函数y=f（x）的解析式；
（2）设数列{an}的前n项和为Sn，Sn=f（n），数列{bn}满足关系式
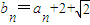，问数列{bn}中是否存在不同的3项，使之成为等比数列？若存在，试写出任意符合条件的3项；若不存在，请说明理由．查看习题详情和答案>>
①存在实数m，使得f（m）=0，且对任意实数x，恒有f（x）≥0成立；
②存在实数k （k≠0），使得f（1-k）=f（1+k）成立．
（1）求函数y=f（x）的解析式；
（2）设数列{an}的前n项和为Sn，Sn=f（n），数列{bn}满足关系式bn=an+2+
| 2 |
（本小题满分13分）已知数列{an}的前n项和为Sn，满足关系式(2＋t)Sn＋1－tSn＝2t＋4(t≠－2，t≠0，n＝1，2，3，…)
(1)当a1为何值时，数列{an}是等比数列；
(2)在(1)的条件下，设数列{an}的公比为f(t)，作数列{bn}使b1＝1，bn＝f(bn－1)(n＝2，
3，4，…)，求bn；
(3)在(2)条件下，如果对一切n∈N＋，不等式bn＋bn＋1＜恒成立，求实数c的取值范围．
查看习题详情和答案>>