网址:http://m.1010jiajiao.com/timu_id_130301[举报]
1. 由函数 知,当
知,当 时,
时, ,且
,且 ,则它的反函数过点(3,4),故选A.
,则它的反函数过点(3,4),故选A.
2.∵ ,∴
,∴ ,则
,则 ,即
,即 ,
, .
. ,选B.
,选B.
3. 由平行四边形法则, ,
,
∴ ,
,
又 ,
,
∴ ,当P为
,当P为 中点时,取得最小值
中点时,取得最小值 .选B.
.选B.
4. 设 是椭圆的一个焦点,它是椭圆三个顶点
是椭圆的一个焦点,它是椭圆三个顶点 ,
, ,
, 构成的三角形的垂心(如图).由
构成的三角形的垂心(如图).由 有
有 ,即
,即 ,∴
,∴ ,得
,得 ,解得
,解得 ,选A.
,选A.
5. 设正方形边长为 ,
, ,则
,则 ,
, .在
.在 由正弦定理得
由正弦定理得
 ,又在
,又在 由余弦定理得
由余弦定理得 ,于是
,于是 ,
, ,选C.
,选C.
 6.
6.  在底面
在底面 上的射影
上的射影 知,
知, 为斜线
为斜线 在平面
在平面 上的射影,∵
上的射影,∵ ,由三垂线定理得
,由三垂线定理得 ,∵
,∵ ,所以直线
,所以直线 与直线
与直线 重合,选A.
重合,选A.
7. 过A作抛物线 的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线
的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线 交右准线于
交右准线于 则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长
则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长 =|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
=|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
由可得两曲线的交点x=,xB∈(,2),
∴3+xB∈(,4),即△ANB周长 取值范围是(,4),选B.
取值范围是(,4),选B.
8. 先将3,5两个奇数排好,有 种排法,再将4,6两个偶数插入3,5中,有
种排法,再将4,6两个偶数插入3,5中,有 种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为
种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为 ,选B.
,选B.
某种型号的汽车在匀速行驶中每小时耗油量 关于行驶速度
关于行驶速度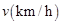 的函数解析式可以表示为:
的函数解析式可以表示为: .已知甲、乙两地相距
.已知甲、乙两地相距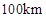 ,设汽车的行驶速度为
,设汽车的行驶速度为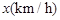 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为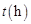 ,耗油量为
,耗油量为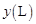 .
.
(1)求函数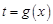 及
及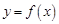 ;
;
(2)求当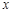 为多少时,
为多少时,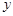 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
【解析】(1) 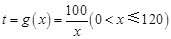 ,根据
,根据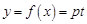 可求出y=f(x).
可求出y=f(x).
(2)求导,根据导数确定其最小值.
查看习题详情和答案>>
设 ,
,  .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)如果存在 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;
(3)如果对任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
【解析】(1)求出切点坐标和切线斜率,写出切线方程;(2)存在 ,
, 转化
转化 解决;(3)任意的
解决;(3)任意的 ,都有
,都有 成立即
成立即 恒成立,等价于
恒成立,等价于 恒成立
恒成立
查看习题详情和答案>>
设数列{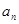 }的前n项和
}的前n项和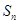 满足:
满足: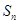 =n
=n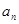 -2n(n-1).等比数列{
-2n(n-1).等比数列{ }的前n项和为
}的前n项和为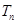 ,公比为
,公比为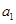 ,且
,且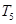 =
=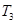 +2
+2 .
.
(1)求数列{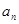 }的通项公式;
}的通项公式;
(2)设数列{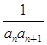 }的前n项和为
}的前n项和为 ,求证:
,求证: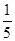 ≤
≤ <
<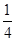 .
.
【解析】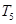 =
=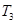 +2
+2 求出
求出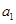 ,由
,由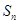 =n
=n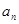 -2n(n-1)递写一个式子相减,得{
-2n(n-1)递写一个式子相减,得{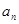 }为等差数列;(2)裂项法求
}为等差数列;(2)裂项法求 ,然后证明
,然后证明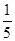 ≤
≤ <
<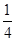 .
.
查看习题详情和答案>>
某市旅游部门开发一种旅游纪念品,每件产品的成本是 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).
(1)写出 与
与 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
【解析】第一问先得到改进工艺后,每件产品的销售价为20(1+x),月平均销售量为 件,则月平均利润
件,则月平均利润 (元),
(元),
∴y与x的函数关系式为

第二问中,求导数,
由 得
得
当 时
时 ;
;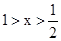 时
时
得到最值。
解:(Ⅰ)改进工艺后,每件产品的销售价为20(1+x),月平均销售量为 件,则月平均利润
件,则月平均利润 (元),
(元),
∴y与x的函数关系式为
 .
.
(Ⅱ)由 得
得
当 时
时 ;
;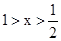 时
时 ,
,
∴函数
在 取得最大值.
取得最大值.
故改进工艺后,产品的销售价为20(1+1/2)=30元时,旅游部门销售该纪念品的月平均利润最大.
查看习题详情和答案>>