网址:http://m.1010jiajiao.com/timu_id_12943[举报]
一、选择题:本大题共10小题,每小题5分,共50分.
1.B.点拔:记命题p的形式为“若A,则B”,则q的形式为“若B,则A”,r的形式为“若.files/image054.gif) B,则
B,则.files/image054.gif) A”,因此,p是r的逆否命题.
A”,因此,p是r的逆否命题.
2.D点拔:∵λ1a+λ2b=λ1(1,2)+λ2(2,3) = (λ1+2λ2+3λ2) = c = (3,4),
∴.files/image057.gif)
3.C点拔:当f′(x)<0时,f(x)递减;当f′(x)>0时,f(x)递增.
4.A点拔:采用插空法,得7×8×9=504.
5.B点拔:∵a3+a6+a9=(a1+a4+a7)+6d, ∴27=39+6d, ∴d=-2.
∵a1+a4+a7=39, ∴3a1+9d=39,得a1=19.
故S9=9a1+.files/image059.gif)
6.D点拔:展开式的通项公式Tr+1=C.files/image061.gif)
令5-2r=-1,得r=3,∴T4=C53?2-2?(-2)3?x-1=-20?.files/image063.gif) 的系数为-20.
的系数为-20.
7.D点拔:设M(x,y),N(0,1),直线MN的倾斜角为α,则可得α∈[0,.files/image065.gif) ]∪[
]∪[.files/image067.gif) ],所以u=
],所以u=.files/image069.gif) [-1,1].
[-1,1].
8.A点拔:设直线l的方程为x = ty+b代入y2 = 8x中,得y2-8ty-8 = 0, ∴y1y2 = -8b.
又∵y1y2=16, ∴-8b=16,b=-2, 直线l的方程为x=ty-2, 过定点A (-2,0)
9.B点拔:∵AC∥EF,EF⊥DE,∴AC⊥DE,又∵AC⊥BD,∴AC⊥平面ABD,∴AC⊥AB,AC⊥AD.∵三棱锥A-BCD为正三棱锥,∴AB、AC、AD两两垂直.
VA-BCD=.files/image071.gif) =
=.files/image073.gif)
10.C点拔:∵f(x+4)=f(-x)=f(x),∴f(x)是以4为周期的周期函数,f(x)=0在区间[-2,18]上的实数根依次为-1,1,3,5,7,…,17,其总和为-1+1+3+5+…+17=-1+.files/image075.gif)
二、填空题:本大题共5小题,每小题5分,共25分.
11.(1,2)点拔:采用根轴法求解.
12.-.files/image077.gif) 点拔:y=
点拔:y=.files/image079.gif) ,∴ymax=
,∴ymax=.files/image081.gif) ,又∵ymax=
,又∵ymax=.files/image083.gif) .令
.令
.files/image085.gif) 则a+b=
则a+b=.files/image087.gif)
13.S.files/image089.gif) ?S△ABH 点拔:易证H为△ABC的垂心.
?S△ABH 点拔:易证H为△ABC的垂心.
.files/image091.jpg) 如图,S
如图,S.files/image089.gif) ?S△ABH.
?S△ABH.
.files/image094.gif)
.files/image096.gif)
14..files/image098.gif) 点拔:P=1-
点拔:P=1-.files/image100.gif)
15.4点拔:∵1*2=3,且2*3=4,
∴.files/image102.gif) ∴x*y=-(6c+1)x+2(c+1)y+cxy.
∴x*y=-(6c+1)x+2(c+1)y+cxy.
由x*m=x恒成立得 -(6c+1)x+2(c+1)m+cmx=x恒成立
即(6c-cm+2)x=2(c+1)m恒成立 ∴.files/image104.gif)
∵m≠0,∴由②得c=-1,代入①,得m=4.
三、解答题:本大题共6小题,共75分.
16.∵|c|=.files/image034.gif) ,∴3sin2
,∴3sin2.files/image107.gif) , ………………(2分)
, ………………(2分)
即.files/image109.gif) ,
,
即3cos(α+β)=cos(α-β), ………………(6分)
即3cosαcosβ-3sinαcosβ=cosαcosβ+sinαsinβ,
即2cosαcosβ=3sinαcosβ
∵a与b不垂直,∴a?b≠0,即cosαcosβ≠0
∴由2sinαsinβ=cosαcosβ得tanαtanβ=.files/image111.gif) ………………(12分)
………………(12分)
17.(Ⅰ)记甲、乙、丙三人独立做对这题的事件分别为A、B、C,
则P(A)=.files/image113.gif)
得P(C)=.files/image115.gif) …………………………………………………………………………(3分)
…………………………………………………………………………(3分)
由P(B?C)=P(B)?P(C)=.files/image040.gif) 得P(B)=
得P(B)=.files/image118.gif)
故乙、丙两人各自做对这道题的概率分别为.files/image118.gif)
.files/image115.gif) ………………………(6分)
………………………(6分)
(Ⅱ)甲、乙、丙三人中至少有两人做对这道题的概率为
P(.files/image120.gif) )
)
=P(.files/image122.gif) )+P(A
)+P(A.files/image124.gif) )+P
)+P.files/image126.gif)
=P(.files/image128.gif) )
).files/image130.gif)
=.files/image132.gif) ………………………(12分)
………………………(12分)
18.(Ⅰ)∵an+an+2=2an+1,∴an-2an+1+an+2=0,即x=-1是方程anx2+2an+1x+an+2=0的相同实数根. ………………………(4分)
(Ⅱ)∵an=a1+(n-1)d=nd,∴方程即为nx2+2(n+1)x+(n+2)=0,
即(nx+n+2)?(x+1)=0,∴cn=-.files/image134.gif) . ……………………(8分)
. ……………………(8分)
(Ⅲ)∵bnbn+1=.files/image136.gif)
∴Sn=4.files/image138.gif) ……(12分)
……(12分)
19.(I)连结AE∵AB=AC,且E为BC的中点,∴AE⊥BC
∵BBl⊥平面ABC,∴AE⊥BBl,∴AE⊥平面BCClBl,
∴平面DBlE⊥平面BCClBl. ………………………………………………(4分)
(Ⅱ)延长AB至F,使AB=BF,连结B1F、EF.
在△EBF中,EF2=BF2+BE2-2BE?BF?cosl35° =16+8―2×4×2.files/image034.gif) ×(-
×(-.files/image050.gif) )=40.
)=40.
B1E2=BBl2+BE2=16+8=24,B1F2=A1B2=32.
在AEBlF中,cos∠EBlF=.files/image142.gif)
∴∠EBl F=arccos
∵B1F∥A1B,∴∠EB1F即为异面直线A1B与B1 E所成的角.
故异面直线A1B与B1E所成的角的大小为arccos.files/image144.gif) ……………………(8分)
……………………(8分)
(Ⅲ)作C1 H⊥B1E于H.∵平面DBlE平面BCClBl,∴C1 H⊥平面DBlE,
∴C1H的长即为点C1到平面DB1E的距离.
∵△B1 HCl∽△B1
BE,∴.files/image146.gif) ∴C1H=
∴C1H=.files/image148.gif)
故点C1到平面DB1E的距离为导.files/image150.gif) .………………………………………(12分)
.………………………………………(12分)
20.(I)铁盒子的底面边长为2a-2x,高为x,容积V=(2a-2x)2?x=4x(a-x)2. …(4分)
(11)∵V=4x3-8ax2+4a2x,∴V′=12x2-16ax+4a2.
令V′=O,得x=.files/image152.gif)
.files/image154.gif) ,或x=a. …………………………………………………(8分)
,或x=a. …………………………………………………(8分)
.files/image156.jpg)
①当0<t<.files/image154.gif) 时,V(x)在(0,t]上是单调增函数,
时,V(x)在(0,t]上是单调增函数,
∴此时V (x)max=V(t)=4t(a-t)2; …………………………………………(11分)
②当.files/image159.gif) ≤t<a时,V(x)max=V(
≤t<a时,V(x)max=V(.files/image154.gif) )=
)=.files/image161.gif) a3. …………………………………(13分)
a3. …………………………………(13分)
21.(I)m+λn=(0,a)+λ(1,0)=(λ,a)=2(1,.files/image163.gif) )(λ≠0),
)(λ≠0),
n+2λm=(1,0)+2λ(0,a)=(1,2λa).
∴两直线的方程分别为y+a=.files/image163.gif) x和y-a=2λax,
x和y-a=2λax,
两式相乘,得y2-2a2x2=a2 …………………………………………………(6分)
当λ=0时,两直线的方程分别为x=0和y=a,交点为P(0,a),
符合方程y2-2a2x2=a2.
综上,得曲线C的方程为y2-2a2x2=a2 ……………………………………(7分)
(Ⅱ)∵a=.files/image050.gif) ,∴点P的轨迹方程为y2-x2=
,∴点P的轨迹方程为y2-x2=.files/image167.gif)
曲线C为双曲线,E(0,1)为双曲线的一个焦点.
①若直线l的斜率不存在,则其方程为x=0,l与双曲线交于M
此时.files/image169.gif) .
……………………………………………………………(8分)
.
……………………………………………………………(8分)
②若直线l的斜率存在,设其方程为y=kx+1,代人y2-x2=.files/image167.gif)
得2(k2-1)x2+4kx+1=0
∵直线l与双曲线交于两点, ∴△=(4k)2-8(k2-1)>0,且k2-1≠0,解得k≠±1.
设M(x1,y1),N(x2,y2),则
.files/image052.gif) =(x1,y1-1)?(x2,y2-1)=(xl,kx1)?(x2,kx2)
=(x1,y1-1)?(x2,y2-1)=(xl,kx1)?(x2,kx2)
=x1x2+k2x1x2=(k2+1)xlx2=.files/image172.gif) .
……………………(11分)
.
……………………(11分)
记.files/image052.gif) =t,则t=
=t,则t=.files/image172.gif) 得k2=
得k2=.files/image175.gif) .
.
∵k≠±1,k2≥0,且k2≠1,∴.files/image175.gif) ≥0,且
≥0,且.files/image175.gif) ≠1,
≠1,
得t>.files/image167.gif) ,或t≤-
,或t≤-.files/image167.gif) ,即
,即.files/image052.gif) ∈(-∞,-
∈(-∞,-.files/image167.gif) )U(
)U(.files/image167.gif) ,+∞).
,+∞).
综上,得.files/image052.gif) 的取值范围是(-∞,
的取值范围是(-∞,.files/image167.gif) )U[
)U[.files/image167.gif) ,+∞].………………(14分)
,+∞].………………(14分)
(本小题满分14分)
在直三棱柱ABC-A1B1C1中,∠ABC=90°, E、F分别为A1C1、B1C1的中点, D为棱CC1上任一点.
(Ⅰ)求证:直线EF∥平面ABD;
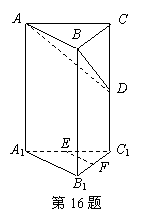 (Ⅱ)求证:平面ABD⊥平面BCC1B1.
(Ⅱ)求证:平面ABD⊥平面BCC1B1.
(本小题满分12分)
直三棱柱A1B1C1—ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点。
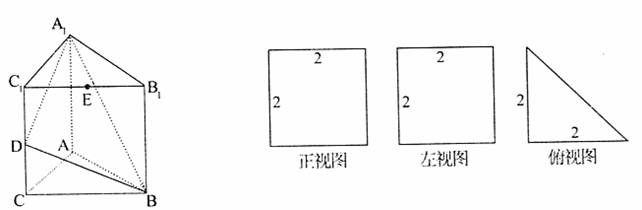
(1)求点B到平面A1C1CA的距离;
(2)求二面角B—A1D—A的余弦值;
(3)在AC上是否存在一点F,使EF⊥平面A1BD,若存在确定其位置,若不存在,说明理由.
查看习题详情和答案>>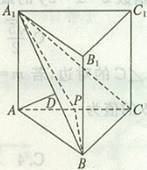 (本小题满分12分) 在直三棱柱
(本小题满分12分) 在直三棱柱