题目内容
（本小题满分12分）
直三棱柱A1B1C1—ABC的三视图如图所示，D、E分别为棱CC1和B1C1的中点。
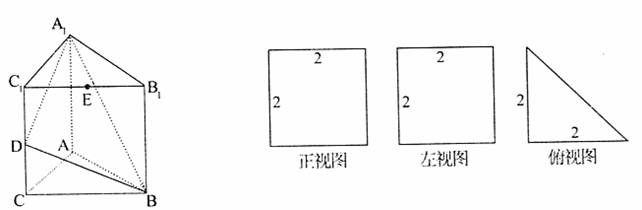
（1）求点B到平面A1C1CA的距离；
（2）求二面角B—A1D—A的余弦值；
（3）在AC上是否存在一点F，使EF⊥平面A1BD，若存在确定其位置，若不存在，说明理由.
解：（1）由已知得：CA=CB=CC1=2，∠ACB=90°
∴BC⊥AC
∴BC⊥平面A1C1CA
∴点B到平面A1C1CA的距离为2……………………………………………………（3分）
（2）如图建立空间直角坐标系
则B（0，2，0）D（0，0，1）A1（2，0，2）
设平面A1DB的法向量为
则
…………………………………………………………………………（6分）
而平面ACC1A1的法向量为
∴二面角B—A1D—A的大小为
……………………………………（8分）
（3）存在F为AC的中点，使EF⊥平面A1BD
设F（x，0，0），由E（0，1，2）得
若EF⊥平面A1BD，则
由得x=1
∴F为AC的中点
∴存在F为AC的中点，使EF⊥平面A1BD………………………………（12分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
