网址:http://m.1010jiajiao.com/timu_id_12840[举报]
一、AADCB DCACB DA
二、(13)160;(14)6π;(15)8;(16)①②③
三、(17)解:(Ⅰ)f(x)=(sinx+cosx)2=[.files\image006.gif) sin(x+
sin(x+.files\image062.gif) ]2=[g(x)]2
]2=[g(x)]2
由f(x)=g(x),得g(x)=0,或g(x)=1
∴.files\image006.gif) sin(x+
sin(x+.files\image062.gif) )=0,或
)=0,或.files\image006.gif) sin(x+
sin(x+.files\image062.gif) )=1……………………………………………3分
)=1……………………………………………3分
∵-.files\image064.gif)
∴x+.files\image062.gif) =0,或x+
=0,或x+.files\image062.gif) =
=.files\image062.gif) ,或x+
,或x+.files\image062.gif) =
=.files\image066.gif)
x=-.files\image062.gif) 或x=0或x=
或x=0或x=.files\image068.gif)
所求x值的集合为{-.files\image062.gif) ,0,
,0,.files\image068.gif) } …………………………………………………7分
} …………………………………………………7分
(Ⅱ)由(Ⅰ)知,.files\image071.gif)
解不等式2kπ+.files\image068.gif) ≤x+
≤x+.files\image062.gif) ≤2kπ+
≤2kπ+.files\image066.gif) ,k∈Z,得
,k∈Z,得
2kπ+.files\image062.gif) ≤x≤2kπ+
≤x≤2kπ+.files\image073.gif) …………………………………………………………9分
…………………………………………………………9分
∵-.files\image068.gif) ≤x≤
≤x≤.files\image068.gif) 且x≠-
且x≠-.files\image062.gif) ,
,
∴.files\image062.gif) ≤x≤
≤x≤.files\image068.gif)
∴函数.files\image047.gif) 的单调递减区间为[
的单调递减区间为[.files\image062.gif) ,
,.files\image068.gif) ]………………………………………12分
]………………………………………12分
18.解:依题意,ξ的可能值为-6000,3000,12000,5000,14000,16000,…2分
P(ξ=-6000)=0.052=0025,
P(ξ=3000)=2×0.2×0.05=0.02,
P(ξ=12000)=0.22=0.4,
P(ξ=5000)=2×0.75×0.05×=0.075,
P(ξ=14000)= 2×0.75×0.2×=0.3,
P(ξ=16000)=0.0752=0.5625…………………………………………………………8分
ξ的分布列为
ξ
-6000
3000
12000
5000
14000
16000
P
0.0025
0.02
0.04
0.075
0.3
0.5625
……………………………………………………………………………………………10分
ξ的期望为
Eξ=-6000×0.0025+3000×0.02+12000×0.04+5000×0.075+14000×0.3+16000×0.5625=14100(元) ………………………………………………………12分
19.解法一:(Ⅰ)∵PO⊥平面ABCD,∴OD为PD在平面ABCD内的射影
又ABCD为菱形,∴AC⊥OD,∴AC⊥PD,即PD⊥AC
在菱形ABCD中,∵∠DAB=60°,
分∴OD=AO?cot60°=1
在Rt△POD中,PD=.files\image076.gif) ,由PE:ED=3:1,得
,由PE:ED=3:1,得
DE=.files\image078.gif) 又∠PDO=60°,
又∠PDO=60°,
∴OE2=OD2+DE2-2OD?DEcos60°=.files\image020.gif)
∴OE2+DE2=OD2,∴∠OED=90°,即PD⊥OE
PD⊥平面EAC…………………………………………………………………………4分
(Ⅱ)由(Ⅰ)知PD⊥EA,PD⊥EC,则∠AEC为二面角A-PD-C的平面角tan∠AEO=.files\image081.gif) ,易知OE为AC的垂直平分线,所以∠AEC=2∠AEO,
,易知OE为AC的垂直平分线,所以∠AEC=2∠AEO,
∴cos∠AEC=cos2∠AEO-sin2∠AEO
=.files\image083.gif) ………………………………………8分
………………………………………8分
(Ⅲ)由O为BD中点,知点B到平面PDC的距离等于点O到平面PDC距离的2倍,由(Ⅰ)知,平面OEC⊥平面PDC,作OH⊥CE,垂足为H,则OH⊥平面PDC,在Rt△OEC中,∠EOC=90°,OC=.files\image085.gif)
∴OH=.files\image087.gif)
所以点B到平面PDC的距离为.files\image089.gif) ……………………………………………12分
……………………………………………12分
.files\image091.jpg) |
解法二:建
立如图所示的坐标系O-xyz,其中A(0,-.files\image051.gif) ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0,.files\image051.gif) ,0),D(-1,0,0),P(0,0,
,0),D(-1,0,0),P(0,0,.files\image051.gif) ).
).
(Ⅰ)由PE:ED=3:1,知E(-.files\image095.gif) )
)
∵.files\image097.gif)
∴.files\image099.gif)
∴PD⊥OE,PD⊥AC,∴PD⊥平面EAC……………………………………………4分
(Ⅱ)由(Ⅰ)知PD⊥EA,PD⊥EC,则∠AEC为二面角A-PD-C的平面角
∵.files\image101.gif)
∴cos∠AEC=cos<.files\image103.gif) ……………………………………………8分
……………………………………………8分
(Ⅲ)由OBD中点知,点B到平面PDC的距离为点O到平面PDC距离的2倍,又.files\image105.gif) ,cos∠OED=cos<
,cos∠OED=cos<.files\image107.gif)
所以点B到平面PDC的距离为
d=2.files\image109.gif) ………………………………………………12分
………………………………………………12分
20.解:(Ⅰ)x-f1(x)=0,即x-.files\image111.gif) ,解得x1=0,x2=1,x3=-1.
,解得x1=0,x2=1,x3=-1.
所以,函数f1(x)的不动点为0,1,-1. ………………………………………………4分
(Ⅱ)令g(x)=x-f2(x)=x-logax(x>0),则g′(x)=1-.files\image113.gif) …………6分
…………6分
(1)若0<a<1,则logae<0,g′(x)>0,则g(x)在(0,+∞)内单调递增.
又g(a)=a-1<0,g(1)=1>0,所以g(x)=0即x-f2(x)=0在(0,1)内有一根. ………………8分
(2)若a>1,则当x∈(0,logae)时,g′<0,g(x)单调递减,当x∈(logae,+∞)时,g′(x)<0,g(x)单调递增;当x=logae时,g(x)有最小值logae-loga(logae).
由g(1)=1>0知,当且仅当logae-loga(logae)≤0时,g(x)=0即x-f2(x)=0有实根.
由a>1,知logae-loga(logae)≤0.files\image115.gif) …………………11分
…………………11分
综合所述,a的取值范围是(0,1)∪(1,e.files\image117.gif) ). …………………………………………12分
). …………………………………………12分
21.解:由已知,F(.files\image119.gif) ),双曲线的渐近线y=±x的方向向量为v=(1,±1),当l斜率k不存在时,不失一般性,取A(
),双曲线的渐近线y=±x的方向向量为v=(1,±1),当l斜率k不存在时,不失一般性,取A(.files\image006.gif) ,-1)、B(
,-1)、B(.files\image006.gif) ,-1)、B(
,-1)、B(.files\image006.gif) ,1),则
,1),则.files\image055.gif) 在v上的投影的绝对值为
在v上的投影的绝对值为.files\image123.gif) ,不合题意 ………………………………………………2分
,不合题意 ………………………………………………2分
所以l的斜率k存在,其方程为y=k(x-.files\image006.gif) ).
).
由.files\image125.gif) 得(k2-1)x2-2
得(k2-1)x2-2.files\image006.gif) k2x+2k2+1=0(k2≠1)
k2x+2k2+1=0(k2≠1)
设A(x1,k(x1-.files\image006.gif) ))、B(x2,k(x2-
))、B(x2,k(x2-.files\image006.gif) )),则x1+x2=
)),则x1+x2=.files\image127.gif) ………………6分
………………6分
当v=(1,1)时,设.files\image055.gif) 与v的夹角为θ,则
与v的夹角为θ,则.files\image055.gif) =(x2-x1,k(x2-x1))在v上投影的绝对值
=(x2-x1,k(x2-x1))在v上投影的绝对值
.files\image131.gif)
=.files\image133.gif)
=.files\image135.gif)
由.files\image137.gif) ,得2k2-5k+2=0,k=2或k=
,得2k2-5k+2=0,k=2或k=.files\image139.gif) .
.
根据双曲线的对称性知,当v=(1,-1)时,k=-2或k=.files\image141.gif) .
.
所以直线l的方程为y=±2(x-.files\image006.gif) )或y=±
)或y=±.files\image144.gif) .…………………12分
.…………………12分
22.解:(Ⅰ)(i)an=1-1+1-…+(-1)n-1=.files\image146.gif) .………………………………3分
.………………………………3分
(ii)用数学归纳法证明:
(1)当n=1时,由f1(x)=1+x,知b1=0,而.files\image148.gif) =0,等式成立. ……4分
=0,等式成立. ……4分
(2)假设当n=k时等式成立,即bk= -.files\image150.gif) ,
,
那么由fk+1(x)=fk(x)[1+(-1)(k+1)-1x]=fk(x)[1+(-1)kx],得
bk+1=bk+(-1)kak=-.files\image152.gif)
=.files\image154.gif)
=-.files\image156.gif)
等式仍然成立. …………………………………………………………………8分
根据(1)和(2)知,对任意n∈N*,都有bn=-.files\image158.gif) ……………………9分
……………………9分
(Ⅱ)cn=1-2+22+…+(-2)n-1=.files\image160.gif) ……………………………11分
……………………………11分
由g1(x)=1-x,知d1=0,
当n≥2时,由gn(x)=gn-1(x)[1+(-2)n-1x],知dn=dn-1+(-2)n-1cn-1,
∴dn-dn-1=(-2)n-1cn-1=(-2)n-1?.files\image162.gif) .
.
∴dn=d1+(d2-d1)+(d3-d2)+…+(-2)(dn-dn-1)
=0+.files\image164.gif)
=.files\image166.gif)
=.files\image168.gif)
=.files\image170.gif)
当n=1时上式也成立.
∴dn=.files\image172.gif) ……………………………………………………14分
……………………………………………………14分
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数;
(3)设A、B是曲线C2上任意不同两点,证明:直线AB与直线y=x必相交.
.(本小题满分12分)
已知以函数f(x)=mx3-x的图象上一点N(1,n)为切点的切线倾斜角为 .
.
(1)求m、n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k-1995,对于x∈[-1,3]恒成立?若存在,求出最小的正整数k,否则请说明理由.
查看习题详情和答案>>
.(本小题满分12分)
已知以函数f(x)=mx3-x的图象上一点N(1,n)为切点的切线倾斜角为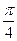 .
.
(1)求m、n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k-1995,对于x∈[-1,3]恒成立 ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由.
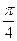 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由.