Question

.(本小题满分12分)

已知以函数f(x)＝mx³－x的图象上一点N(1，n)为切点的切线倾斜角为.

(1)求m、n的值；

(2)是否存在最小的正整数k，使得不等式f(x)≤k－1995，对于x∈[－1,3]恒成立？若存在，求出最小的正整数k，否则请说明理由．

 

Answer 1

【答案】

解：(1)f′(x)＝3mx²－1，

f′(1)＝tan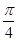＝1，

 

∴3m－1＝1，∴m＝.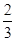

 

从而由f(1)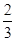＝－1＝n，得n＝－，

 

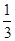∴m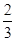＝，n＝－.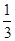

(2)存在．

f′(x)＝2x²－1＝2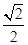(x＋)(x－)，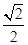

 

令f′(x)＝0得x＝±.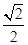

 

在[－1,3]中，当x∈[－1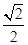，－]时，

 

f′(x)＞0，f(x)为增函数，

当x∈[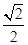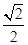－，]时，

 

f′(x)＜0，f(x)为减函数，

此时f(x)在x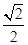＝－时取得极大值．

 

当x∈[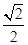，3]时，

 

此时f′(x)＞0，f(x)为增函数，

比较f(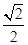－)，f(3)知f(x)_max＝f(3)＝15.

 

∴由f(x)≤k－1995，知15≤k－1995，

∴k≥2010，即存在最小的正整数k＝2010，

使不等式在x∈[－1,3]上恒成立．

【解析】略