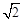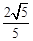网址:http://m.1010jiajiao.com/timu_id_12315[举报]
一、1.B 2.B 3.D 4.B 5.D 6.A 7.B 8.C 9.B 10.B 11.B 12.D
二、13. 14.32 15.162 16.3
三、17.解:(1)
(2)
,
18.解:(1)设5次实验中只成功一次为事件A,一次都不成功为事件B,
则P(5次实验至少2次成功)=1-P(A)-P(B)=1-
(法2:所求概率为)
(2)ξ的可能取值为2、3、4、5
又
19.解法1:(1)取CD的中点E,连结PE、EM、EA
∵△PCD为正三角形 ∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
∵平面PCD⊥平面ABCD ∴PE⊥平面ABCD
∵四边形ABCD是矩形 ∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得EM=,AM=,AE=3 ∴EM2+AM2=AE2
∴∠AME=90° ∴AM⊥PM
(2)由(1)可知EM⊥AM,PM⊥AM ∴∠PME是二面角P―AM―D的平面角
∴tan∠PME= ∴∠PMA=45° ∴二面角P―AM―D为45°
(3)设D点到平面PAM的距离为d,连结DM,则
在Rt△PEM中,由勾股定理可求得PM=,,
解法2:(1)以D点为原点,
分别以直线DA、DC
为x轴、y轴,建立
如图所示的空间直角
坐标系D―xyz,
依题意,可得D(0,0,0),P(0,1,),C(0,2,0),A(2,0,0),
M(,2,0),
即,∴AM⊥PM.
(2)设平面PAM,则
取y=1,得 显然平面ABCD
.
结合图形可知,二面角P―AM―D为45°;
(3)设点D到平面PAM的距离为d,由(2)可知)与平面PAM垂直,
则
即点D到平面PAM的距离为
20.解:(1)
①当时 由
解得:定义域为(0,+∞)
∴函数的单调递增区间为(
由可知的单调递增区间为
②当时 同理可得:函数的单调递增区间为
函数的单调递减区间为
(2)当时,
令
当上单调递增
当上单调递减
又在[1,3]上连续 为函数的极大值.
又
是函数在[1,3]上的最小值,
为在[1,3]的最大值.
21.解:(1)在直线
∵P1为直线l与y轴的交点,∴P1(0,1) ,
又数列的公差为1
(2)
(3)
是以2为公比,4为首项的等比数列,
22.解:(1)直线l过点(3,)且方向向量为)
∴l方程为 化简为:
∵直线和椭圆交于两点和x轴交于M(1,0)
又
即
(2) ∴椭圆C方程为
由
∴椭圆C方程为:
(3)将中得 ①
由韦达定理知:
由②2/③知:………④
对方程①求判别式,且由 即
化简为:………………⑤
由④式代入⑤式可知:,求得,
又椭圆的焦点在x轴上,则,
由④知:,结合,求得
因此所求椭圆长轴长2a范围为(2,).
 ,则
,则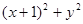 的最小值为( )
的最小值为( )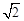 B.2 C.
B.2 C. D.
D.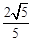
 ,则
,则 的最小值为( )
的最小值为( )


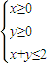 ,则
,则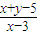 的最大值为( )
的最大值为( ) ,则
,则 的最大值为( )
的最大值为( )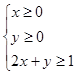 ,则
,则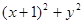 的最小值为( )
的最小值为( )